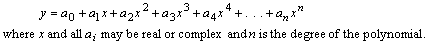|
Constructors
|
public ComplexPoly(int n)
|
|
|
public ComplexPoly(Complex[] a)
|
|
public ComplexPoly(float[] a)
|
|
|
public ComplexPoly(double[] a)
|
|
public ComplexPoly(int[] a)
|
|
public ComplexPoly(ArrayList<Object> a)
|
|
public ComplexPoly(Polynomial a)
|
|
|
public ComplexPoly(Complex a)
|
|
|
public ComplexPoly(double a)
|
|
|
public ComplexPoly(Complex a, Complex b)
|
|
|
public ComplexPoly(double a, double b)
|
|
|
public ComplexPoly(Complex a, Complex b, Complex c)
|
|
|
public ComplexPoly(double a, double b, double c)
|
|
|
public ComplexPoly(Complex a, Complex b, Complex c, Complex d)
|
|
|
public ComplexPoly(double a, double b, double c, double d)
|
|
|
Set Values
|
public void resetPoly(Complex[] aa)
|
|
|
public void resetPoly(ArrayList<Object> aa)
|
|
|
public void resetCoeff(int i, Complex aa)
|
|
|
|
public static ComplexPoly rootsToPoly(Complex[] roots)
|
|
Get Values
|
public Complex[] polyNomCopy()
|
|
|
public Complex[] polyNomReference()
|
|
|
public Complex coeffCopy(int i)
|
|
|
public Complex coeffReference(int i)
|
|
|
public int getDeg()
|
|
|
Deep Copy
|
public ComplexPoly copy()
|
public static ComplexPoly copy(ComplexPoly aa)
|
|
public Object clone()
|
|
Check if highest order
coefficient is zero
|
public ComplexPoly reducePoly()
|
public static ComplexPoly reducePoly(ComplexPoly aa)
|
|
Convert Polynomial to a String
|
public String toString()
|
|
|
public void seti()
|
|
|
public void setj()
|
|
|
Print to the screen
|
public void print()
|
|
|
public void println()
|
|
|
Write to a Text File
|
public void printToText(String title)
|
|
|
public void printToText()
|
|
|
Addition
|
public ComplexPoly plus(ComplexPoly b)
|
public static ComplexPoly plus(ComplexPoly a, ComplexPoly b)
|
|
public ComplexPoly plus(Complex b)
|
public static ComplexPoly plus(ComplexPoly a, Complex b)
|
|
public ComplexPoly plus(double b)
|
public static ComplexPoly plus(ComplexPoly a, double b)
|
|
public ComplexPoly plus(int b)
|
public static ComplexPoly plus(ComplexPoly a, int b)
|
|
Subtraction
|
public ComplexPoly minus(ComplexPoly b)
|
public static ComplexPoly minus(ComplexPoly a, ComplexPoly b)
|
|
public ComplexPoly minus(Complex b)
|
public static ComplexPoly minus(ComplexPoly a, Complex b)
|
|
public ComplexPoly minus(double b)
|
public static ComplexPoly minus(ComplexPoly a, double b)
|
|
public ComplexPoly minus(int b)
|
public static ComplexPoly minus(ComplexPoly a, int b)
|
|
Multiplication
|
public ComplexPoly times(ComplexPoly b)
|
public static ComplexPoly times(ComplexPoly a, ComplexPoly b)
|
|
public ComplexPoly times(Complex b)
|
public static ComplexPoly times(ComplexPoly a, Complex b)
|
|
public ComplexPoly times(double b)
|
public static ComplexPoly times(ComplexPoly a, double b)
|
|
nth derivative
|
public ComplexPoly nthDerivative(int n)
|
|
|
Evaluate Polynomial or a Derivative
|
public Complex evaluate(Complex x)
|
|
|
public Complex evaluate(double x)
|
|
|
public Complex nthDerivEvaluate(int n, Complex x)
|
|
|
public Complex nthDerivEvaluate(int n, double x)
|
|
|
Equality test
|
public boolean equals(ComplexPoly cp)
|
|
|
public boolean isEqual(ComplexPoly cp)
|
public static boolean isEqual(ComplexPoly cp1, ComplexPoly cp2)
|
|
Roots
|
public Complex[] roots()
|
|
|
public Complex[] roots(boolean polish)
|
|
|
public Complex[] roots(Complex estx)
|
|
|
public Complex[] roots(boolean polish, Complex estx)
|
|
|
public static Complex[] quadratic(Complex a, Complex b, Complex c)
|
public static Complex[] quadratic(double a, double b, double c)
|
|
|
public static Complex[] cubic(Complex a, Complex b, Complex c, Complex d)
|
|
|
public static Complex[] cubic(double a, double b, double c, double d)
|
|
public Complex[] laguerreAll()
|
|
|
public Complex[] laguerreAll(boolean polish)
|
|
|
public Complex[] laguerreAll(Complex estx)
|
|
|
public Complex[] laguerreAll(boolean polish, Complex estx)
|
|
|
|
public static Complex laguerre(Complex estx, Complex[] coeff, int deg)
|
|
|
public static void resetTestConverge(double newtest)
|
|
|
public static double getTestConverge()
|
|
|
public static ComplexPoly rootsToPoly(Complex[] roots)
|