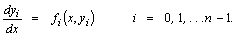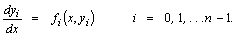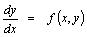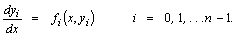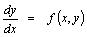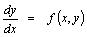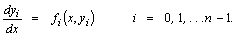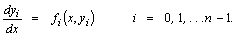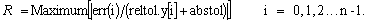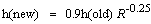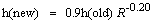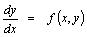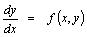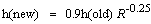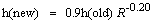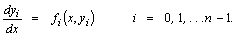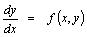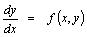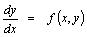|
Constructor
|
public RungeKutta()
|
|
Set initial value of x
|
public void setInitialValueOfX(double x0)
|
|
Set final value of x
|
public void setFinalValueOfX(double xn)
|
|
Set initial value/s of y
|
public void setInitialValueOfY(double y0)
|
|
public void setInitialValuesOfY(double[] y0)
|
|
Set step size / initial step size
|
public void setStepSize(double step)
|
|
Set tolerance (accuracy)
|
public void setToleranceScalingFactor(double tolSF)
|
|
public void setToleranceAdditionFactor(double tolAddn)
|
|
Number of iterations
|
public void setMaximumIterations(int maxIter)
|
|
public int getNumberOfIterations()
|
|
public static void resetNstepsMultiplier(int multiplier)
|
|
4th order Runge-Kutta
| Single ODE, single x value
|
public double fourthOrder(DerivFunction g)
|
|
public static double fourthOrder(DerivFunction g, double x0, double y0, double xn, double h)
|
|
Single ODE, several x values
|
public double[][] fourthOrder(DerivFunction g, int nPoints)
|
|
public double[][] fourthOrder(DerivFunction g, double[] points)
|
|
public static double [][] fourthOrder(DerivFunction g, int nPoints, double x0, double y0, double xn, double h)
|
|
public static double [][] fourthOrder(DerivFunction g, double[] points, double x0, double y0, double xn, double h)
|
| Several ODEs, single x value
|
public double[] fourthOrder(DerivnFunction g)
|
|
public static double[ ] fourthOrder(DerivnFunction g, double x0, double[ ] y0, double xn, double h)
|
| Several ODEs, several x values
|
public double[][] fourthOrder(DerivnFunction g, int nPoints)
|
|
public double[][] fourthOrder(DerivnFunction g, double[] points)
|
|
public static double [][] fourthOrder(DerivnFunction g, int nPoints, double x0, double y0, double xn, double h)
|
|
public static double [][] fourthOrder(DerivnFunction g, double[] points, double x0, double y0, double xn, double h)
|
|
Runge-Kutta-Cash-Karp
|
Single ODE, single x value
|
public double cashKarp(DerivFunction g)
|
|
public static double cashKarp(DerivFunction g, double x0, double y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double cashKarp(DerivFunction g, double x0, double y0, double xn, double h, double abstol, double reltol)
|
|
Single ODE, several x values
|
public double[][] cashKarp(DerivFunction g, int nPoints)
|
|
public double[][] cashKarp(DerivFunction g, double[] points)
|
|
public static double[][] cashKarp(DerivFunction g, int nPoints, double x0, double y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double[][] cashKarp(DerivFunction g, double points, double x0, double y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double[][] cashKarp(DerivFunction g, int nPoints, double x0, double y0, double xn, double h, double abstol, double reltol)
|
|
public static double[][] cashKarp(DerivFunction g, double points, double x0, double y0, double xn, double h, double abstol, double reltol)
|
|
Several ODEs, single x value
|
public double[] cashKarp(DerivnFunction g)
|
|
public static double[] cashKarp(DerivnFunction g, double x0, double[ ] y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double[] cashKarp(DerivnFunction g, double x0, double[ ] y0, double xn, double h, double abstol, double reltol)
|
|
Several ODEs, several x values
|
public double[][] cashKarp(DerivnFunction g, int nPoints)
|
|
public double[][] cashKarp(DerivnFunction g, double[] points)
|
|
public static double[][] cashKarp(DerivnFunction g, int nPoints, double x0, double y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double[][] cashKarp(DerivnFunction g, double points, double x0, double y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double[][] cashKarp(DerivnFunction g, int nPoints, double x0, double y0, double xn, double h, double abstol, double reltol)
|
|
public static double[][] cashKarp(DerivnFunction g, double points, double x0, double y0, double xn, double h, double abstol, double reltol)
|
|
Runge-Kutta-Fehlberg
|
Single ODE, single x value
|
public double fehlberg(DerivFunction g)
|
|
public static double fehlberg(DerivFunction g, double x0, double y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double fehlberg(DerivFunction g, double x0, double y0, double xn, double h, double abstol, double reltol)
|
|
Single ODE, several x values
|
public double[][] fehlberg(DerivFunction g, int nPoints)
|
|
public double[][] fehlberg(DerivFunction g, double[] points)
|
|
public static double[][] fehlberg(DerivFunction g, int nPoints, double x0, double y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double[][] fehlberg(DerivFunction g, double points, double x0, double y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double[][] fehlberg(DerivFunction g, int nPoints, double x0, double y0, double xn, double h, double abstol, double reltol)
|
|
public static double[][] fehlberg(DerivFunction g, double points, double x0, double y0, double xn, double h, double abstol, double reltol)
|
|
Several ODEs, single x value
|
public double[] fehlberg(DerivnFunction g)
|
|
public static double[ ] fehlberg(DerivnFunction g, double x0, double[ ] y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double[ ] fehlberg(DerivnFunction g, double x0, double[ ] y0, double xn, double h, double abstol, double reltol)
|
|
Several ODEs, several x values
|
public double[][] fehlberg(DerivnFunction g, int nPoints)
|
|
public double[][] fehlberg(DerivnFunction g, double[] points)
|
|
public static double[][] fehlberg(DerivnFunction g, int nPoints, double x0, double y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double[][] fehlberg(DerivnFunction g, double points, double x0, double y0, double xn, double h, double abstol, double reltol, int maxiter)
|
|
public static double[][] fehlberg(DerivnFunction g, int nPoints, double x0, double y0, double xn, double h, double abstol, double reltol)
|
|
public static double[][] fehlberg(DerivnFunction g, double points, double x0, double y0, double xn, double h, double abstol, double reltol)
|
| Return the x and y values for all steps between the initial and final points |
public double[][] getAllValues()
|
| Plots |
Plot a multipoint output |
public void plot()
|
| Plot all step values |
public void plotSteps()
|