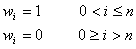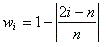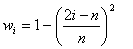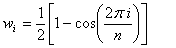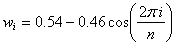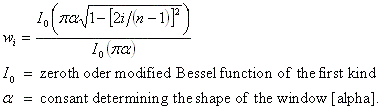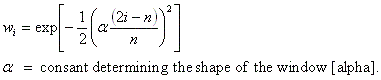| |
Michael Thomas Flanagan's Java Scientific Library
FourierTransform Class: Fourier Transforms
|
|
|
Last update: 7 July 2008
Main Page of Michael Thomas Flanagan's Java Scientific Library
This class contains the method for performing a Fast Fourier Transform (FFT) and associated methods, e.g. for obtaining an estimation of a power spectrum, for correlating data, for windowing data, for obtaining short time Fourier transform time-frequency representations (STFT / Spectrogram-FT). The basic fast fourier transform procedure is adapted from the Numerical Recipes method written in the C language (Numerical Recipes in C, The Art of Scientific Computing, W.H. Press, S.A. Teukolsky, W.T. Vetterling & B.P. Flannery, Cambridge University Press, 2nd Edition (1992) pp 496 - 558, http://www.nr.com/.
import directive: import flanagan.math.FourierTransform;
SUMMARY OF CONSTRUCTORS AND METHODS
|
Constructors
|
public FourierTransform()
|
public FourierTransform(double[] data)
|
public FourierTransform(Complex[] data)
|
|
Input the data array to be transformed
|
as a real data array
|
public void setData(double[] data)
|
|
as a complex data array (as Complex numbers)
|
public void setData(Complex[] data)
|
|
as complex data array (as alternating real and imaginary parts)
|
public void setFftData(double[] fftData)
|
|
Fast Fourier transform
|
Perform transform
|
public void transform()
|
|
Perform inverse transform
|
public void inverse()
|
|
Basic fft method
|
public void basicFft(double[] data, int nn, int isign)
|
|
Get the transformed data
|
as Complex
|
public Complex[] getTransformedDataAsComplex()
|
|
as alternating real and imaginary
|
public double[] getTransformedDataAsAlternate()
|
|
Get the original data
|
as Complex
|
public Complex[] getComplexInputData()
|
|
as alternating real and imaginary
|
public double[] getAlternateInputData()
|
|
Get data length
|
data length used
|
public int getUsedDataLength()
|
original data length
|
public int getOriginalDataLength()
|
|
Check data length
|
as integer power of two
|
public static boolean checkPowerOfTwo(int n)
|
as integer times an integer power of two
|
public static int checkIntegerTimesPowerOfTwo(int n)
|
Get nearest lower integer power of two
|
public static int lastPowerOfTwo(int n)
|
Get nearest higher integer power of two
|
public static int nextPowerOfTwo(int n)
|
|
Windowing the data
|
Choose window function
|
public void setRectangular()
public void setBartlett()
public void setWelch()
public void setHann()
public void setHamming()
public void setKaiser(double alpha)
public void setKaiser()
public void setGaussian(double alpha)
public void setGaussian()
|
|
Remove the window function
|
public void removeWindow()
|
|
Get the current window option
|
public String getWindowOption()
|
|
Get the window function weights
|
public double[] getWindowWeights()
|
|
Sampling period
|
|
public void setDeltaT(double deltaT)
public double getDeltaT()
|
|
Power Spectrum
|
Number of segments
|
public void setSegmentNumber(int nSeg)
public int getSegmentNumber()
|
|
Segment length
|
public void setSegmentLength(int length)
public int getSegmentLength()
|
|
Choose overlap option
|
public void setOverLapOption(boolean option)
public boolean getOverLapOption()
|
|
Generate power spectrum
|
public double[][] powerSpectrum()
public double[][] powerSpectrum(String inputFileName)
|
|
Get power spectral density (psd) estimates
|
public double[][] getPowerSpectrumEstimate()
|
|
Print the psd estimates to a text file
|
public void printPowerSpectrum(String outputFileName)
public void printPowerSpectrum()
|
|
Display graph of the result
|
public void plotPowerSpectrum(String graphName)
public void plotPowerSpectrum(int lowPoint, String outputFileName)
public void plotPowerSpectrum(int lowPoint, int highPoint, String outputFileName)
public void plotPowerSpectrum(double lowFreq, String outputFileName)
public void plotPowerSpectrum(double lowFreq, double highFreq, String outputFileName)
public void plotPowerSpectrum()
public void plotPowerSpectrum(int lowPoint)
public void plotPowerSpectrum(int lowPoint, int highPoint)
public void plotPowerSpectrum(double lowFreq)
public void plotPowerSpectrum(double lowFreq, double highFreq)
|
|
Display log graph of the result
|
public void plotPowerLog(String graphName)
public void plotPowerLog(int lowPoint, String outputFileName)
public void plotPowerLog(int lowPoint, int highPoint, String outputFileName)
public void plotPowerLog(double lowFreq, String outputFileName)
public void plotPowerLog(double lowFreq, double highFreq, String outputFileName)
public void plotPowerLog()
public void plotPowerLog(int lowPoint)
public void plotPowerLog(int lowPoint, int highPoint)
public void plotPowerLog(double lowFreq)
public void plotPowerLog(double lowFreq, double highFreq)
|
|
Get number of psd points
|
public int getNumberOfPsdPoints()
|
|
Calculate required number of data points
|
public static int calcDataLength(boolean overlap, int segLen, int segNum)
|
|
Correlation
|
Correlate two data sets
|
public double[][] correlate(double[] data)
public double[][] correlate(double[] data1, double[] data2)
|
|
Get the correlation array
|
public double[][] getCorrelation()
|
|
Print the correlation to a text file
|
public void printCorrelation(String outputFileName)
public void printCorrelation()
|
|
Display graph of the correlation
|
public void plotCorrelation(String graphName)
public void plotCorrelation()
|
|
Change line option in graphs
|
|
public void setPlotLineOption(int lineOption)
public int getPlotLineOption()
|
Short Time Fourier Transform
- Spectrogram
(Time-Frequency Representation)
|
Generate Short Time Fourier Transform
|
public double[][] shortTime(int windowLength)
public double[][] shortTime(double windowTime)
|
|
Get Time-Frequency Matrix
|
public double[][] getTimeFrequencyMatrix()
|
|
Plot Time-Frequency Contour Map
|
public void plotShortTime(String graphTitle)
public void plotShortTime()
|
|
Print Time-Frequency Transform to file
|
public void printShortTime(String fileName)
public void printShortTime()
|
|
Get window length
|
public int getShortTimeWindowLength()
|
|
Get number of sample times
|
public int getShortTimeNumberOfTimes()
|
|
Get number of frequencies
|
public int getShortTimeNumberOfFrequencies()
|
CONSTRUCTORS
public FourierTransform()
public FourierTransform(Complex[] data)
public FourierTransform(double[] data)
Usage:
FouierTransform ft = new FourierTransform();
This creates a new instance, in this example, ft, of FourierTransform().
Usage:
FouierTransform ft = new FourierTransform(data);
This creates a new instance, in this example, ft, of FourierTransform() and initilises this instance with the data to be transformed. This data may be real or complex.
METHODS
INPUT THE DATA TO BE TRANSFORMED
The data to be transformed may be provided via the Constructor (see above) or by one of the following methods.
public void setData(Complex[] data)
public void setData(double[] data)
Usage:
ft.setData(x);
The data may be provided as the argument of the method, setData, as either an array of real (double) or complex (Complex) numbers, x in the above usage.
public void setFftData(double[] fftData)
Usage:
ft.fftData(y);
The data may also be provided as an array of alternating real and imaginary parts of each complex number in the sequence of complex numbers to be transformed, i.e. in the above example, the double y[0] is the real part of the first complex number, y[1] is the imaginary part of the first complex number, y[2] is the real part of the second complex number and so on. This is input form has been included for compatability with other fft applications. All methods in this class will accept data entered in any of the three above forms.
FAST FOURIER TRANSFORM
Perform a Fourier Transform
public void transform()
Usage:
ft.transform();
This is the standard method, in this class, for performing a fast Fourier transform (fft). The data length must be a power of two; a warning mesage will be printed to screen if it is not and the data array will be first padded with zeros until a length equal to an integer power of two is reached. The transformed data may be accessed via getTransformedDataAsComplex() or getTransformedDataAsAlternate().
Perform an inverse Fourier Transform
public void inverse()
Usage:
ft.inverse();
This is the standard method, in this class, for performing an inverse fast Fourier transform (fft). The data length must be a power of two; a warning mesage will be printed to screen if it is not and the data array will be first padded with zeros until a length equal to an integer power of two is reached. The transformed data may be accessed via getTransformedDataAsComplex() or getTransformedDataAsAlternate().
public void basicFft(double[] data, int nn, int isign)
Usage:
ft.basicFft(data, nn, isign);
This is the basic fft method accessed by both transform and inverse described above. It is based on the Numerical Recipes, C method, four1. This method would not normally be called directly but if it is the data must be in the form of alternating real and imaginary parts, as described in the third data input method descibed above. The integer nn must equal half the length of the data array data, i.e. must equal the number of complex numbers in the data to be transformed. The integer nn must be a power of 2. This method, basicFfft, does not check this. If the integer isign is set to 1 the the array data is overwritten with its discreet Fourier transform. If the integer isign is set to -1 the the array data is overwritten with nn times its inverse discreet Fourier transform. The transformed data is returned as an array of alternating real and imaginary parts of the complex transformed data. No data is returned by this method to the instance variable data arrays.
GET THE TRANSFORMED DATA
Get the transformed data as Complex
public Complex[] getTransformedDataAsComplex()
Usage:
tData = ft.getTransformedDataAsComplex();
This method returns the transformed data as an array of complex numbers. The data is ordered as:
| tData[0] | | frequency = 0 |
| tData[1] | | frequency = 1/(n.deltaT) |
| tData[2] | | frequency = 2/(n.deltaT) |
| . . . . . . | | . . . . . . |
| tData[n/2-1] | | frequency = (n/2 - 1)/(n.deltaT) |
| tData[n/2] | | frequency = aliased combination/(2.deltaT) |
| tData[n/2+1] | | frequency = -(n/2-1)/(n.deltaT) |
| tData[n/2+2] | | frequency = -(n/2-2)/(n.deltaT) |
| . . . . . . | | . . . . . . |
| tData[n-1] | | frequency = -1/(n.deltaT) |
where n is the number of data points, deltaT is the sampling period which is set to 1 if has not been set to the actual value by setDeltaT, and the aliased combination point contains the real and imaginary parts of the one aliased point that contains the most positive and the most negative frequency.
Get the transformed data as alternating real and imaginary parts
public double[] getTransformedDataAsAlternate()
Usage:
tData = ft.getTransformedDataAsAlternate();
This method returns the transformed data as an array of alternating real and imaginary parts of the transformed complex data. The data is ordered as:
| tData[0] | | real part | | frequency = 0 |
| tData[1] | | imaginary part | | frequency = 0 |
| tData[2] | | real part | | frequency = 1/(n.deltaT) |
| tData[3] | | imaginary part | | frequency = 1/(n.deltaT) |
| tData[4] | | real part | | frequency = 2/(n.deltaT) |
| tData[5] | | imaginary part | | frequency = 2/(n.deltaT) |
| . . . . . . | | . . . . . . | | . . . . . . |
| tData[n-2] | | real part | | frequency = (n/2 - 1)/(n.deltaT) |
| tData[n-1] | | imaginary part | | frequency = (n/2-1)/(n.deltaT) |
| tData[n] | | real part | | frequency = aliased combination/(2.deltaT) |
| tData[n+1] | | imaginary part | | frequency = aliased combination/(2.deltaT) |
| tData[n+2] | | real part | | frequency = -(n/2-1)/(n.deltaT) |
| tData[n+3] | | imaginary part | | frequency = -(n/2-1)/(n.deltaT) |
| tData[n+2] | | real part | | frequency = -(n/2-2)/(n.deltaT) |
| tData[n+3] | | imaginary part | | frequency = -(n/2-2)/(n.deltaT) |
| . . . . . . | | . . . . . . | | . . . . . . |
| tData[2n-2] | | real part | | frequency = -1/(n.deltaT) |
| tData[2n-1] | | imaginary part | | frequency = -1/(n.deltaT) |
where n is the number of data points, deltaT is the sampling period which is set to 1 if has not been set to the actual value by setDeltaT, and the aliased combination points contain the real and imaginary parts of the one aliased point that contains the most positive and the most negative frequency.
GET THE ORIGINAL DATA
Get the original data as Complex
public Complex[] getComplexInputData()
Usage:
oData = ft.getComplexInputData();
This method returns the original data as an array of complex numbers.
Get the original data as alternating real and imaginary parts
public double[] getAlternateInputData()
Usage:
tData = ft.getAlternateInputData();
This method returns the original data as an array of alternating real and imaginary parts of the original complex data.
GET THE DATA LENGTH
Get the data length used
public int getUsedDataLength()
Usage:
lenUsed = ft.getUsedDataLength();
This method returns the length of the data array used in obtaining the transform. It may differ from the original data length as a result of point deletion (to give an even number) or zero padding to give a length that is an integer power of two.
Get the original data length
public int getOriginalDataLength()
Usage:
lenOrig = ft.getOriginalDataLength();
This method returns the original length of the data array to be used in obtaining a transform. It may differ from the actual data length used as a result of point deletion (to give an even number) or zero padding to give a length that is an integer power of two.
CHECK THE DATA LENGTH
Check that a data length is an integer power of two
public static boolean checkPowerOfTwo(int n)
Usage:
test = FourierTransform.checkPowerOfTwo(n);
This method returns true if the integer n is an integer power of two and returns false if it is not.
Check that a data length is an integer multiplied by an integer power of two
public static int checkIntegerTimesPowerOfTwo(int n)
Usage:
mult = FourierTransform.checkIntegerTimesPowerOfTwo(n);
This method checks if the integer n is an integer times an integer power of two and returns the integer multiplier if it is. It returns zero if it is not.
Get the nearest lower integer that is an integer power of two
public static int lastPowerOfTwo(int n)
Usage:
lower = FourierTransform.lastPowerOfTwo(n);
This method returns the nearest integer power of two that is equal to or lower than argument, n.
Get the nearest higher integer that is an integer power of two
public static int nextPowerOfTwo(int n)
Usage:
higher = FourierTransform.nextPowerOfTwo(n);
This method returns the nearest integer power of two that is equal to or higher than argument, n.
WINDOWING THE DATA
Choose a window function
public void setRectangular()
Usage:
ft.setRectangular();
This method applies a rectangular window (also called square or box-car window) to the data,
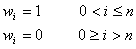
where w is the window function weight, 0 is the first point in the segment and n is the last point in the segment.
This is the default option if no window function is set.
public void setBartlett()
Usage:
ft.setBartlett();
This method applies a Bartlett window, i.e. a triangular window, to the data,
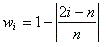
where w is the window function weight, 0 is the first point in the segment and n is the last point in the segment.
public void setWelch()
Usage:
ft.setWelch();
This method applies a Welch window to the data,
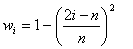
where w is the window function weight, 0 is the first point in the segment and n is the last point in the segment.
public void setHann()
Usage:
ft.setHann();
This method applies a Hann window (also called a van Hann or Hanning window) to the data,
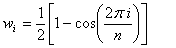
where w is the window function weight, 0 is the first point in the segment and n is the last point in the segment.
public void setHamming()
Usage:
ft.setHamming();
This method applies a Hamming window to the data,
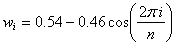
where w is the window function weight, 0 is the first point in the segment and n is the last point in the segment.
public void setKaiser(double alpha)
public void setKaiser()
Usage:
ft.setKaiser(alpha);
This method applies a Kaiser window to the data,
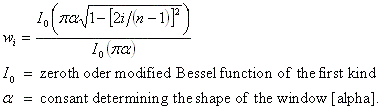
where w is the window function weight, 0 is the first point in the segment and n is the last point in the segment.
Usage:
ft.setKaiser();
This method applies a Kaiser window to the data,
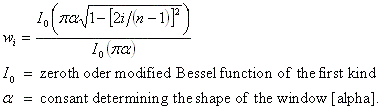
where w is the window function weight, 0 is the first point in the segment and n is the last point in the segment and a default value of 2.0 is assigned to constant, alpha.
public void setGaussian(double alpha)
public void setGaussian()
Usage:
ft.setGaussian(alpha);
This method applies a Gaussian window to the data,
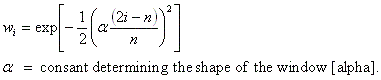
where w is the window function weight, 0 is the first point in the segment and n is the last point in the segment. The constant, alpha, must be equal to or greater than 2.0.
Usage:
ft.setGaussian();
This method applies a Gaussian window to the data,
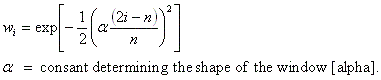
where w is the window function weight, 0 is the first point in the segment and n is the last point in the segment and a default value of 2.5 is assigned to constant, alpha.
Remove the current window option
public void removeWindow()
Usage:
ft.removeWindow();
This method removes the current window option and replaces it with the rectangular window option.
get the window function weightsS
public double[] getWindowWeights()
Usage:
weights = ft.getWindowWeights();
This method returns the array of Window function weights, i.e. the w described above.
Get the current window option
public String getWindowOption()
Usage:
opt = ft.getWindowOption();
This method returns the Window function option as a String, e.g, "Rectangular". See immediately above for description of options.
OBTAIN AN ESTIMATION OF A POWER SPECTRUM
Set the number of segments
public void setSegmentNumber(int nSeg)
Usage:
ft.setSegmentNumber(nSeg);
The number of the segments used in powerSpectrum is set by this method. If the length of the segment and hence the number of segments have already been set by calling setSegmentLength that calculated number will be overwritten by this later call to setSegmentNumber. If neither setSegmentNumber nor setSegmentLength are called the default value of the segment number is one and the default value of the segment length is the full data length.
public int getSegmentNumber()
Usage:
nSeg = ft.getSegmentNumber();
The number of the segments used in powerSpectrum is returned by this method.
Set the segment length
public void setSegmentLength(int length)
Usage:
ft.setSegmentLength(length);
The length of the segments used in powerSpectrum is set by this method. If the number of segments and hence the length of the segment has already been set by calling setSegmentNumber that calculated length will be overwritten by this later call to setSegmentLength. If neither setSegmentLength nor setSegmentNumber are called the default value of the segment length is the full data length and the default value of the segment number is one.
public int getSegmentLength()
Usage:
length = ft.getSegmentLength();
The length of the segments used in powerSpectrum is returned by this method.
Choose the overlap option
public void setOverLapOption(boolean option)
Usage:
ft.setOverLapOption(option);
This method sets the data segment overlap option to be used by the method obtaining a power spectrum.
If:
- option = true; overlap by half segment length. This gives the smallest spectral variance per data point. It is good where data already recorded and data reduction is after the process.
- option = false; no overlap. This gives the smallest spectral variance per computer operation. This is good for real time data collection where data reduction is computer limited. This is the default option when an instance of FourierTransform is created.
public boolean getOverLapOption()
Usage:
opt = ft.getOverLapOption();
This method returns the overlap option. See immediately above for description of options.
Generate a power spectrum estimation
public double[][] powerSpectrum()
public double[][] powerSpectrum(String inputFileName )
Usage:
psdEstimates = ft.powerSpectrum();
This method generates an estimation of a power spectrum of the windowed data first entered by the constructor or one of the data setting methods.
The data may be segmented and the segments may be overlapped.
If no segmentation is set, either by calling setSegmentNumber or setSegmentLength, the entered data is transformed as a single block. If its length is not an integer power of two this method looks for the largest subset that can be transformed either as a single block or as overlapped or non-overlapped segments. It then checks whether the number of points deleted to acheive this is less than the number of zeros needed to pad the data to a length equal to an integer power of two. If it is then the subset is transformed accordingly. If it is not the zero padded data is transformed as a single block.
If the data is segmented the segment length is checked both for length (an integer power of two) and for integer divisibility (first divided by two if overlap required) into the total data length. If either test fails the data is transformed as a single block with the above checks listed for non-segmented data.
The estimations of the power spectral densities (psd) are returned as the mean square amplitude for each frequency equal to i/(segment length) cycles per grid point or cycles per unit time if the time interval (delta t) has been set. The frequencies are returned in the first row of the returned array, e.g. psdEstimates[0][[0], psdEstimates[0][[1], etc and the psd estimates are returned in the second row, e.g. psdEstimates[1][[0], psdEstimates[1][[1], etc.
Usage:
psdEstimates = ft.powerSpectrum(inputFileName);
This method generates an estimation of a power spectrum of the windowed data entered, as the transform proceeds, from a text file (.txt), whose name is entered as this method's argument, inputFileName. Only one segment at a time is read in and only one segment is ever stored. The text file format is simply the data ordered as alternating real and imaginary parts:
real part (data point 0) imaginary part (data point 0)
real part (data point 1) imaginary part (data point 1)
real part (data point 2) imaginary part (data point 2)
. . . .
The data may be segmented and the segments may be overlapped.
If no segmentation is set, either by calling setSegmentNumber or setSegmentLength, the entered data is transformed as a single block.
Unlike powerSpectrum() (see above) limited data checking is performed on the data read in from a text file. The segment length is checked and if it is not an integer power of two the program is aborted. It is assumed that, in setting up the text file, the user has checked that the division into segments has been calculated correctly.
The estimations of the power spectral densities (psd) are stored as the mean square amplitude for each frequency equal to i/(segment length) cycles per grid point or cycles per unit time if the time interval (delta t) has been set. The frequencies are returned in the first row of the returned array, e.g. psdEstimates[0][[0], psdEstimates[0][[1], etc and the psd estimates are returned in the second row, e.g. psdEstimates[1][[0], psdEstimates[1][[1], etc.
Get the estimated power spectral dendities (psd)
public double[][] getPowerSpectrumEstimate()
Usage:
result = ft.getPowerSpectrumEstimate();
This method also returns the array of power spectral densities (psd) of the the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName) (see above).
Print the estimated power spectrum to a text file
public void printPowerSpectrum(outputFileName)
public void printPowerSpectrum()
Usage:
ft.printPowerSpectrum(outputfilename);
This method prints the power spectrum estimation generated by powerSpectrum() or powerSpectrum(inputFileName) to a text file whose name is held in the String outputTextFile. The output file is a time and date stamped text file listing the transform details and the mean square amplitudes at each frequency equal to i/(segment length) cycles per grid point or per unit time if the sampling period has been set.
Usage:
ft.printPowerSpectrum();
This method prints the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName) to a text file named FourierTransformPSD.txt. The output file is a time and date stamped text file listing the transform details and the mean square amplitudes at each frequency equal to i/(segment length) cycles per grid point or cycles per unit time if the sampling period has been set.
Display a graph of the estimated power spectrum
public void plotPowerSpectrum(String graphName)
public void plotPowerSpectrum(int lowPoint, String outputFileName)
public void plotPowerSpectrum(int lowPoint, int highPoint, String outputFileName)
public void plotPowerSpectrum(double lowFreq, String outputFileName)
public void plotPowerSpectrum(double lowFreq, double highFreq, String outputFileName)
public void plotPowerSpectrum()
public void plotPowerSpectrum(int lowPoint)
public void plotPowerSpectrum(int lowPoint, int highPoint)
public void plotPowerSpectrum(double lowFreq)
public void plotPowerSpectrum(double lowFreq, double highFreq)
Usage:
ft.plotPowerSpectrum(graphTitle);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName) as a plot of the mean square amplitude against cycles per grid point or cycles per unit time if the sampling period has been set. The plot is given the title held in the String graphTitle.
Usage:
ft.plotPowerSpectrum(lowPoint, graphTitle);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from point lowPoint to the highest point, as a plot of the mean square amplitude against cycles per grid point or cycles per unit time if the sampling period has been set. For example, ft.plotPowerSpectrum(1, graphTitle) would display all points except the first point i.e. point 0 [Java indices start at 0]. The plot is given the title held in the String graphTitle.
Usage:
ft.plotPowerSpectrum(lowPoint, highPoint, graphTitle);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from point lowPoint to point, highPoint, [Java indices start at 0] as a plot of the mean square amplitude against cycles per grid point or cycles per unit time if the sampling period has been set. The plot is given the title held in the String graphTitle.
Usage:
ft.plotPowerSpectrum(lowFreq, graphTitle);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from the frequency lowFreq to the highest frequency, as a plot of the mean square amplitude against cycles cycles per unit time. The sampling period must have been set if this method is to be called. If lowFreq is set equal to -1.0D the first point, i.e. the zero frequency point, will be ignored. The plot is given the title held in the String graphTitle.
Usage:
ft.plotPowerSpectrum(lowFreq, highFreq, graphTitle);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from the frequency lowFreq to the frequency, highFreq, as a plot of the mean square amplitude against cycles cycles per unit time. The sampling period must have been set if this method is to be called. If lowFreq is set equal to -1.0D the first point, i.e. the zero frequency point, will be ignored. The plot is given the title held in the String graphTitle.
Usage:
ft.plotPowerSpectrum();
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName) as a plot of the mean square amplitude against cycles per grid point or cycles per unit time if the sampling period has been set. The plot is given the title "Estimation of Power Spectrum".
Usage:
ft.plotPowerSpectrum(lowPoint);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from point lowPoint to the highest point, as a plot of the mean square amplitude against cycles per grid point or cycles per unit time if the sampling period has been set. For example, ft.plotPowerSpectrum(1) would display all points except the first point i.e. point 0 [Java indices start at 0]. The plot is given the title "Estimation of Power Spectrum".
Usage:
ft.plotPowerSpectrum(lowPoint, highPoint);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from point lowPoint to point, highPoint, [Java indices start at 0] as a plot of the mean square amplitude against cycles per grid point or cycles per unit time if the sampling period has been set. The plot is given the title "Estimation of Power Spectrum".
Usage:
ft.plotPowerSpectrum(lowFreq);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from the frequency lowFreq to the highest frequency, as a plot of the mean square amplitude against cycles cycles per unit time. The sampling period must have been set if this method is to be called. If lowFreq is set equal to -1.0D the first point, i.e. the zero frequency point, will be ignored. The plot is given the title "Estimation of Power Spectrum".
Usage:
ft.plotPowerSpectrum(lowFreq, highFreq);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from the frequency lowFreq to the frequency, highFreq, as a plot of the mean square amplitude against cycles cycles per unit time. The sampling period must have been set if this method is to be called. If lowFreq is set equal to -1.0D the first point, i.e. the zero frequency point, will be ignored. The plot is given the title "Estimation of Power Spectrum".
Display a log graph of the estimated power spectrum
public void plotPowerLog(String graphName)
public void plotPowerLog(int lowPoint, String outputFileName)
public void plotPowerLog(int lowPoint, int highPoint, String outputFileName)
public void plotPowerLog(double lowFreq, String outputFileName)
public void plotPowerLog(double lowFreq, double highFreq, String outputFileName)
public void plotPowerLog()
public void plotPowerLog(int lowPoint)
public void plotPowerLog(int lowPoint, int highPoint)
public void plotPowerLog(double lowFreq)
public void plotPowerLog(double lowFreq, double highFreq)
Usage:
ft.plotPowerLog(graphTitle);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName) as a plot of the log10(mean square amplitude) against cycles per grid point or per unit time if the sampling period has been set. Amplitudes of zero value are ignored, i.e. in effect, set equal to the minimum non-zero amplitude. The plot is given the title held in the String graphTitle.
Usage:
ft.plotPowerLog(lowPoint, graphTitle);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from point lowPoint to the highest point, as a plot of the log10(mean square amplitude) against cycles per grid point or cycles per unit time if the sampling period has been set. For example, ft.plotPowerLog(1, graphTitle) would display all points except the first point i.e. point 0 [Java indices start at 0]. Amplitudes of zero value are ignored, i.e. in effect, set equal to the minimum non-zero amplitude. The plot is given the title held in the String graphTitle.
Usage:
ft.plotPowerLog(lowPoint, highPoint, graphTitle);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from point lowPoint to point, highPoint, [Java indices start at 0] as a plot of the log10(mean square amplitude) against cycles per grid point or cycles per unit time if the sampling period has been set. Amplitudes of zero value are ignored, i.e. in effect, set equal to the minimum non-zero amplitude. The plot is given the title held in the String graphTitle.
Usage:
ft.plotPowerLog(lowFreq, graphTitle);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from the frequency lowFreq to the highest frequency, as a plot of the log10(mean square amplitude) against cycles cycles per unit time. The sampling period must have been set if this method is to be called. If lowFreq is set equal to -1.0D the first point, i.e. the zero frequency point, will be ignored. Amplitudes of zero value are ignored, i.e. in effect, set equal to the minimum non-zero amplitude. The plot is given the title held in the String graphTitle.
Usage:
ft.plotPowerLog(lowFreq, highFreq, graphTitle);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from the frequency lowFreq to the frequency, highFreq, as a plot of the log10(mean square amplitude) against cycles cycles per unit time. The sampling period must have been set if this method is to be called. If lowFreq is set equal to -1.0D the first point, i.e. the zero frequency point, will be ignored. Amplitudes of zero value are ignored, i.e. in effect, set equal to the minimum non-zero amplitude. The plot is given the title held in the String graphTitle.
Usage:
ft.plotPowerLog();
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName) as a plot of the log10(mean square amplitude) against cycles per grid point or per unit time if the sampling period has been set. Amplitudes of zero value are ignored, i.e. in effect, set equal to the minimum non-zero amplitude. The plot is given the title "Estimation of Power Spectrum".
Usage:
ft.plotPowerLog(lowPoint);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from point lowPoint to the highest point, as a plot of the log10(mean square amplitude) against cycles per grid point or cycles per unit time if the sampling period has been set. For example, ft.plotPowerLog(1) would display all points except the first point i.e. point 0 [Java indices start at 0]. Amplitudes of zero value are ignored, i.e. in effect, set equal to the minimum non-zero amplitude. The plot is given the title "Estimation of Power Spectrum".
Usage:
ft.plotPowerLog(lowPoint, highPoint);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from point lowPoint to point, highPoint, [Java indices start at 0] as a plot of the log10(mean square amplitude) against cycles per grid point or cycles per unit time if the sampling period has been set. Amplitudes of zero value are ignored, i.e. in effect, set equal to the minimum non-zero amplitude. The plot is given the title "Estimation of Power Spectrum".
Usage:
ft.plotPowerLog(lowFreq);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from the frequency lowFreq to the highest frequency, as a plot of the log10(mean square amplitude) against cycles per unit time. The sampling period must have been set if this method is to be called. If lowFreq is set equal to -1.0D the first point, i.e. the zero frequency point, will be ignored. Amplitudes of zero value are ignored, i.e. in effect, set equal to the minimum non-zero amplitude. The plot is given the title "Estimation of Power Spectrum".
Usage:
ft.plotPowerLog(lowFreq, highFreq);
This method displays a graph the power spectrum generated by powerSpectrum() or powerSpectrum(inputFileName), from the frequency lowFreq to the frequency, highFreq, as a plot of the log10(mean square amplitude) against cycles per unit time. The sampling period must have been set if this method is to be called. If lowFreq is set equal to -1.0D the first point, i.e. the zero frequency point, will be ignored. Amplitudes of zero value are ignored, i.e. in effect, set equal to the minimum non-zero amplitude. The plot is given the title "Estimation of Power Spectrum".
Get the number of points in the generated power spectrum estimation
public int getNumberOfPsdPoints()
Usage:
nPsd = ft.getNumberOfPsdPoints();
This method returns the number of points in the returned power spectrum. This number is equal to half the segment length used in the transform.
Sampling period
public void setDeltaT(double deltaT)
Usage:
ft.setDeltaT(deltaT);
This method sets the value of the sampling period. This method is optional. If the value of the sampling period has been set, it is used by the graphing and printing methods to convert the cycles per unit grid point to a true frequency.
public double getDeltaT()
Usage:
deltaT = ft.getDeltaT);
This method returns the value of the sampling period if this has been set.
Calculation of the required number of data points
public static int calcDataLength(boolean overlap, int segLen, int segNum)
Usage:
FourierTransform.calcDataLength(overlap, segLen, segNum);
This static method calculates the number of data points that would be required by powerSpectrum for a given overlap option, overlap, a given segment length, segLen and a given number of segments, segNum.
If overlap = true:
number of data points required = (number of segments + 1)*(segment length)/2
If overlap = false:
number of data points required = (number of segments)*(segment length)
CORRELATION
Correlate two data sets
public double[][] correlate(double[] data)
public double[][] correlate(double[] data1, double[] data2)
Usage:
correlation = ft.correlate(data);
Returns the correlation beween two sets of real data of equal length, n. The first set must have previusly been entered via a constructor or a setrData method. The second data set is supplied as the argument of this method, (data in the above usage). The two data sets must be of the same length which must be an integer power of two. The returned two dimensional array of doubles, of length, n-1 contains the correlation coefficients at each lag time in the second row, i.e. correlation[1][0], correlation[1][1], etc and the lag times in the first row, i.e. correlation[0][0], correlation[0][1], etc. It is ordered as:
| Array Index | | Lag time |
| 0 | | -(n/2 - 1).deltaT | |
| 1 | | -(n/2 - 2).deltaT | |
| . . . . . . | | . . . . . . | |
| n/2 - 2 | | -deltaT | |
| n/2 - 1 | | 0 | |
| n/2 | | +deltaT | |
| . . . . . . | | . . . . . . | |
| n - 2 | | +(n/2 - 2).deltaT
|
| n - 1 | | +(n/2 - 1).deltaT | |
If the sampling period, deltaT has not been set (see Sampling period) deltaT is put equal to unity, i.e. the lag is in grid point units. The sign convention of this method is that if the data already entered lags the data passed as the method argument, i.e. is shifted to the right of it, a peak will be displayed as a positive lag.
Usage:
correlation = ft.correlate(data1, data2);
Returns the correlation beween two sets of real data of equal length, n, both supplied as arguments of this method, (data1 and data2 in the above usage). The two data sets must be of the same length which must be an integer power of two. The returned two dimensional array of doubles, of length, n-1 contains the correlation coefficients at each lag time in the second row, i.e. correlation[1][0], correlation[1][1], etc and the lag times in the first row, i.e. correlation[0][0], correlation[0][1], etc. It is ordered in the same manner as described immediately above. The sign convention of this method is that if the data1 lags data2, i.e. is shifted to the right of it, a peak will be displayed as a positive lag.
Get the correlation array
public double[][] getCorrelation()
Usage:
correlation = ft.getCorrelataion();
This method also returns the array of correlation coefficients generated by correlare(data) or correlate(data1, data2) (see above for description of array contents).
Print the correlation to a text file
public void printCorrelation(outputFileName)
public void printCorrelation()
Usage:
ft.printCorrelation(outputfilename);
This method prints the correlation generated by correlate(data) or correlate(data1, data2) to a text file whose name is held in the String outputTextFile. The output file is a time and date stamped text file listing the transform details and the correlation coefficients at each time lag.
Usage:
ft.printCorrelate();
This method prints the correlation generated by correlate(data) or correlate(data1, data2) to a text file named Correlation.txt.. The output file is a time and date stamped text file listing the transform details and the correlation coefficients at each time lag.
Display a graph of the correlation
public void plotCorrelation(graphTitle)
public void plotCorrelation()
Usage:
ft.plotCorrelation(graphTitle);
This method displays a graph the correlation coefficients generated by correlate(data) or correlate(data1, data2) as a plot of the correlation coefficients against the lag times (as grid intervals or time units if the sampling period has been set). The plot is given the title held in the String graphTitle.
Usage:
ft.plotCorrelation();
This method displays a graph the correlation coefficients generated by correlate(data) or correlate(data1, data2) as a plot of the correlation coefficients against the lag times (as grid intervals or time units if the sampling period has been set). The plot is given the title "Correlation Plot".
LINE OPTION IN GRAPH PLOTTING METHODS
Change the line option
public void setPlotLineOption(double lineOption)
Usage:
ft.setPlotLineOption(lineOption);
This method resets the line option used in plotPowerSpectrum and plotCorrelation(). The options are:
- lineOption = 0 Points are linked by straight lines [default value]
- lineOption = 1 Points are linked by a cubic spline interpolation
- lineOption = 2 No line is drawn - only point markers
Get the line option
public int getPlotLineOption()
Usage:
lineOption = ft.getPlotLineOption();
This method gets the line option used in plotPowerSpectrum and plotCorrelation(). See immediately above for option descriptions.
SHORT TIME FOURIER TRANSFORM - SPECTROGRAM
Generate a spectrogram
public double[][] shortTime(int windowLength)
public double[][] shortTime(double windowTime)
Usage:
timeFrequency = ft.shortTime(windowLength);
Returns a time frequency matrix for a short-time Fourier Transform of the data entered via a construcor or set data method (see above) with a moving window of a number of data points equal to the argument, windowLength. This length must be an integer power of two. The window set by one of the set window methods (see above) is applied to the moving window of this method. If no window function has been set a Gaussian window with alpha = 2.5 is applied. Elements 1 onwards of the first row of the returned matrix, i.e. timeFrequency[0][1], timeFrequency[0][2]... , contain the avearge time of the window, as time units if the sampling period, deltaT, has been set, or grid point averages if not. Elements 1 onwards of the first column, i.e. timeFrequency[1][0], timeFrequency[2][0]... , contain the frequencies, as cycles per unit time if the sampling period, deltaT, has been set, or as cycles per grid point if not. the zeroth, zeroth element, i.e. timeFrequency[0][0], is blank. All other elements contain the square amplitudes for each window position and each frequency, i.e. timeFrequency[i][j] contains the mean square amplitude for the frequency, timeFrequency[i][0], and the window centred on a time, timeFrequency[0][j].
Usage:
timeFrequency = ft.shortTime(windowTime);
Returns a time frequency matrix for a short-time Fourier Transform of the data entered via a construcor or set data method (see above) with a moving window of a length, in time, equal to the argument, windowTime. This length is converted to the corresponding number of data points. If this number is not an integer power of two it is replaced by the nearest integer power of two. The window set by one of the set window methods (see above) is applied to the moving window of this method. If no window function has been set a Gaussian window with alpha = 2.5 is applied. Elements 1 onwards of the first row of the returned matrix, i.e. timeFrequency[0][1], timeFrequency[0][2]... , contain the avearge time of the window, as time units if the sampling period, deltaT, has been set, or grid point averages if not. Elements 1 onwards of the first column, i.e. timeFrequency[1][0], timeFrequency[2][0]... , contain the frequencies, as cycles per unit time if the sampling period, deltaT, has been set, or as cycles per grid point if not. the zeroth, zeroth element, i.e. timeFrequency[0][0], is blank. All other elements contain the square amplitudes for each window position and each frequency, i.e. timeFrequency[i][j] contains the mean square amplitude for the frequency, timeFrequency[i][0], and the window centred on a time, timeFrequency[0][j].
Get the Time-Frequency Matrix
public double[][] getTimeFrequencyMatrix()
Usage:
timeFrequency = ft.getTimeFrequencyMatrix();
This method also returns the time-frequency matrix generated by shortTime(window) (see immediately above for description of array contents).
Print the Time-Frequency matrix to a text file
public void printShortTime(String fileName)
public void printShortTime()
Usage:
ft.printShortTime(outputfilename);
This method prints the time-frequency matrix generated by shortTime(window) to a text file whose name is held in the String outputTextFile. The output file is a time and date stamped text file listing the transform details and the time frequency matrix. If there are more than 127 window times average values are taken to give 100 columns.
Usage:
ft.printshortTime();
This method prints the time-frequency matrix generated by shortTime(window) to a text file named ShortTime.txt. The output file is a time and date stamped text file listing the transform details and the time frequency matrix. If there are more than 127 window times average values are taken to give 100 columns.
Plot Time-Frequency Contour Map
public void plotShortTime(String graphTitle)
public void plotShortTime()
Usage:
ft.plotShortTime(graphTitle);
This method displays a contour plot the squared amplitudes of the time-frequency matrix generated by shortTime(window). The plot is given the title held in the String graphTitle.
Usage:
ft.plotShortTime();
This method displays a contour plot the squared amplitudes of the time-frequency matrix generated by shortTime(window)
Get the Short-Time Fourier Transform window length
public int getShortTimeWindowLength()
Usage:
windowLength = ft.getShortTimeWindowLength();
This method returns the short-time Fourier transform window length, last used, as number of data points in the window.
Get the number of Short-Time Fourier Transform sample times
public int getShortTimeNumberOfTimes()
Usage:
sampleN = ftgetShortTimeNumberOfTimes();
This method returns the number of sample times in the short-time Fourier transform.
Get the number of Short-Time Fourier Transform frequencies
public int getShortTimeNumberOfFrequencies()
Usage:
freqN = ft.getShortTimeNumberOfFrequencies();
This method returns the number of frequencies in the short-time Fourier transform output.
OTHER CLASSES USED BY THIS CLASS
This class uses the following classes in this library:
This page was prepared by Dr Michael Thomas Flanagan