Introduction
Liquid crystals are an intermediate phase of matter existing between
the crystalline solid and amorphous liquids. They retain orientational
order on melting from the solid form, but can flow readily like
a liquid, and become totally disordered in the high temperature
fluid phase. Liquid crystalline states arise in materials with molecules
that possess geometric anisotropy, either
being rod or disc shaped. The ordering of these molecules gives
rise to anisotropy of the electric and optical properties.
Liquid Crystal Phases
Liquid crystals can be broadly categorized as either lyotropic
and thermotropic. Lyotropic liquid crystal molecules comprise a
hydrophobic tail and a hydrophilic head and form liquid crystal
phases when dissolved in a polar solvent. The molecules assemble
so that the tails group together, exposing the hydrophilic heads
to the solvent. A wide range of phases can be formed, for example
the micellar or lamellar phase (molecules form bilayers separated
by solvent). Phase transitions are induced by changes to the solvent
concentration or to the temperature. For very specific combinations
of molecules and solvent concentrations, micelles can form that
are not spherical, which can give rise to liquid crystal phases
that are similar to those seen in thermotropic liquid crystals.
Thermotropic liquid crystals typically are formed from pure compounds
or mixtures of rod or disc shaped molecules and give rise to liquid
crystal hases over a fixed temperature range. Generally speaking,
there are three liquid crystal phases, known as the smectic, nematic
and cholesteric phases.
Ordinary liquids generally possess some short-range order on a
molecular scale but lack any macroscopic order. This is known as
the isotropic phase. If a liquid crystal is heated sufficiently
it will become isotropic. On cooling there will be a transition
temperature, where various degrees of ordering of the fluid give
rise to a liquid crystal phase, specifically the nematic phase.
Further cooling can gives rise to another liquid crystal phase,
called the smectic phase, which not only posses orientational order
but also a degree of positional ordering. When the temperature falls
beneath the melting point the crystalline solid forms, where the
molecules are rigidly bound in both space and orientation.
Nematic Phase
The simplest of the liquid crystal phases is the nematic phase.
In this phase the molecules behave much like those of a liquid,
being free to move and with no positional order, but differ in the
respect that the molecules tend to align with one another. The director
can change from point to point, and is a function of space. The
word nematic is derived from the Greek nematos meaning thread like,
referring to thread-like structures that can be
observed when these materials are viewed using a polarising microscope.
This phase of liquid crystal is used in virtually all commercially
available liquid crystal displays. Most nematic liquid crystals
are uniaxial, meaning that the major of axis of the molecules tend
to align with each other. Biaxial nematics also orient along a secondary
axis.
Smectic Phase
Smectic liquid crystals are closest in structure to solid crystals
and posses a high degree of order, with diffuse positional order
as well as orientational order. The additional smectic order results
in the formation of layered structures. There are several classes
of a smectic material depending on the in layer ordering and the
angle between the layer normal and the director (labelled A, B,
C, and so on, according to the chronological sequence of
their detection). The most common smectic materials are smectic
A, where the director is parallel to the layer normal, and smectic
C, where the director is at an angle to the layer normal. Smectic
materials show wax like properties, whereas nematic materials flow
more freely making them more suitable for liquid crystal displays.
Chiral Phase
The chiral nematic phase replaces the nematic phase when the molecules
lack inversion symmetry. The chiral component of the molecular interaction
produces a helical twisted structure of pitch 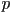 , which
can be as short as , which
can be as short as 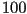 nm [2]. The helical twist may be
clockwise or anti-clockwise, depending on the molecular conformation. nm [2]. The helical twist may be
clockwise or anti-clockwise, depending on the molecular conformation.
The helical structure of the chiral nematic phase has the ability
to selectively reflect light of a wavelength equal to that of the
helical pitch length; however, in order for this to happen the material
must be aligned so that the helical axes are parallel to the light
propagation direction. A common commercial application for this
type of phase is in thermochromic thermometer devices and other
devices that change colour with temperature.The tilted smectic phases
can also be chiral, where the director rotates about the cone between
the layer normal and the tilt. The chiral version of the smectic
A phase is referred to as the 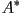 phase. phase.
Properties of Liquid Crystals
As a result of the uniaxial symmetry, the dielectric constants
differ in the value along the preferred axis (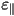 )
and perpendicular to this axis ( )
and perpendicular to this axis (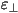 ). The
dielectric anisotropy ( ). The
dielectric anisotropy (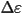 ) is the difference
between the parallel and perpendicular dielectric constants. When
an electric field is applied to a liquid crystal, the induced ) is the difference
between the parallel and perpendicular dielectric constants. When
an electric field is applied to a liquid crystal, the induced
dipole moment of the molecules creates a net torque which tends
to align the molecules along the direction of the electric field.
This is true for molecules with a positive dielectric anisotropy.This
uniaxial symmetry also gives rise to anisotropy in the refractive
index. For this reason a glass flask filled with
nematic LC often appears as an opaque fluid, as light is scattered
due to the fluctuations in refractive index. The ordinary refractive
index no, is for light with electric field polarisation perpendicular
to the director, and the extraordinary refractive index ne, is for
light with electric field polarisation parallel to the director.
The birefringence is the difference between these
two values. The viscosity of fluid is the internal resistance to
flow, defined
as the ratio of the shearing stress to the rate of shear. A flow
process induces a favoured director orientation, and conversely
a field-induced reorientation of the director induces a flow effect.
A detailed analysis of the liquid crystal requires 5 independent
viscous coefficients, but usually the behaviour is approximated
using a single rotational viscosity coefficient (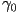 ). ).
Phase Transitions and Orientational Order
A phase transition is the transformation of a thermodynamic system
from one phase to another. At the transition, a small change in
thermodynamic variable such as the temperature or pressure result
an abrupt change in one or more physical properties. An example
is the transition between solid, liquid and gaseous phases. Here,
the transition can be characterised by an abrupt change in density.
When a liquid crystal is cooled from the isotropic state to the
nematic there is a reduction in symmetry and an associated (abrupt)
increase in order at the phase transition. This transition can be
characterised as first-order, as it involves a latent heat; an amount
of energy is absorbed or released during
the transformation between phases. First-order transitions are associated
with "mixed-phase regimes"; in which some parts of the system have
completed the transition and others have not. To quantify this behaviour
it is necessary to introduce the concept of an order parameter.
If we define a unit vector to represent the long axis of each
molecule, described by a distribution function 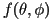 ,
then the director is the statistical average of these unit vectors
over a small volume element around a point. A measure of the fluctuation
in these vectors about the director is defined by the order parameter
S, which is usually based on the average of the second Legendre
polynomial: S=<\frac{1}{2}\cos^2 \theta - 1>
where ,
then the director is the statistical average of these unit vectors
over a small volume element around a point. A measure of the fluctuation
in these vectors about the director is defined by the order parameter
S, which is usually based on the average of the second Legendre
polynomial: S=<\frac{1}{2}\cos^2 \theta - 1>
where 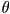 is the angle between the long axis of an individual
molecule and the director is the angle between the long axis of an individual
molecule and the director 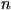 and the angular brackets denote
a statistical average. Due to the head tail symmetry of the molecules
the first order polynomial vanishes and cannot be used. Equivalently: and the angular brackets denote
a statistical average. Due to the head tail symmetry of the molecules
the first order polynomial vanishes and cannot be used. Equivalently:
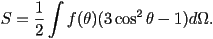
If  is zero everywhere except for at is zero everywhere except for at  and and  then the molecules are all aligned
parallel to one another and then the molecules are all aligned
parallel to one another and 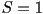 , corresponding to a crystalline
state. If the orientation is completely random , corresponding to a crystalline
state. If the orientation is completely random 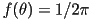 ,
integrating the last equation leads to ,
integrating the last equation leads to 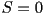 , the isotropic
state. In the nematic phase, the order parameter takes intermediate
value that typically ranges from , the isotropic
state. In the nematic phase, the order parameter takes intermediate
value that typically ranges from 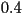 to to 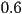 . It
is possible for this equation to yield . It
is possible for this equation to yield 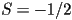 if if 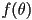 is peaked at
is peaked at 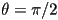 , however this corresponds the
unlikely situation where a collection of rods favour perpendicular
alignment. The order parameter can be measured in a number of ways,
for example by optical birefringence or Raman scattering. , however this corresponds the
unlikely situation where a collection of rods favour perpendicular
alignment. The order parameter can be measured in a number of ways,
for example by optical birefringence or Raman scattering.
This definition has the problem that the isotropic state is not
the only molecular configuration that can give the state of minimum
order parameter. If the molecules are arranged in a cone about the
director with a specific angle, 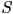 can equal zero [1,p.17].
Additional order parameters can be defined using higher order Legendre
polynomials, which can remove this ambiguity, however, for the purposes
of modelling it is convenient restrict the definition to second-order. can equal zero [1,p.17].
Additional order parameters can be defined using higher order Legendre
polynomials, which can remove this ambiguity, however, for the purposes
of modelling it is convenient restrict the definition to second-order.
The majority of liquid crystal phases are uniaxial in the bulk,
with a single degree of rotational symmetry about the director.
The search for a liquid crystal that is biaxial in the bulk has
been the subject of much research, and only recently have such phases
been created, made possible by molecules possessing bent cores.
It is possible to have a uniaxial or biaxial arrangement of biaxial
molecules. Biaxial molecules can be pictured as being in shape like
a plank of wood. Both short and long axis of the molecules can posses
orientational order, a biaxial arrangement. It is also possible
that only the long axes exhibit orientational order and the short
axes are randomly orientated, or vice versa.
This is a uniaxial arrangement.
Uniaxial molecules can also form uniaxial or biaxial arrangements.
In the uniaxial arrangement the long axes of the molecules align
with each other. The biaxial arrangement of uniaxial is the most
difficult configuration to picture, but is important as it arises
in proximity to disclinations. This state can be induced by an applied
electric field or by constrained geometries, where there are two
directions in which the long axes of the molecules tend to align.
The previous definition of order parameter was in terms of angle,
but it useful to define the order in terms of an order tensor.
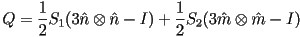
Using the Spectral Theorem
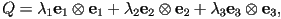
where 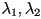 and and 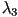 are the
eigenvalues of are the
eigenvalues of 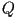 and and 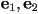 and
and 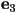 are the corresponding eigenvectors. are the corresponding eigenvectors.
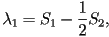
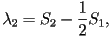
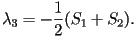
When two eigenvalues are equal this represents a uniaxial state,
corresponding to one of three possible cases; 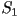 only
is nonzero, only only
is nonzero, only 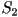 only is nonzero or finally only is nonzero or finally 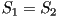 .
When all three eigenvalues differ this represents a biaxial state.
The isotropic state occurs when all the eigenvalues are identically
zero. .
When all three eigenvalues differ this represents a biaxial state.
The isotropic state occurs when all the eigenvalues are identically
zero.
[1] E. G. Virga, "Variational theories for liquid crystals",
ser. Applied mathematics and
mathematical computation. London: Chapman & Hall, 1994
[2] P. J. Collings and M. Hird, "Introduction to liquid crystals
: chemistry and physics", ser. The liquid crystals book series.
London: Taylor & Francis, 1997.
This page last modified
6 October, 2006
by r.james
|
![]() +44 (0)20 7679 2000 - Copyright © 1999-2005 UCL
+44 (0)20 7679 2000 - Copyright © 1999-2005 UCL