|
| INFORMATION FOR Prospective Students INFORMATION Home PROJECTS Funded QUICK LINKS Optical Devices
|
Liquid Crystal Hydrodynamics with Variable Order
TheoryThe order and the orientation of the liquid crystal are represented by a symmetric and traceless tensor, the Q-tensor:
where The equilibrium Q-tensor field minimizes the Landau-de Gennes (LdG) free energy functional:
where
where The surface contribution takes the form [2] This is an anisotropic anchoring energy; a different energy penalty
can be assigned to azimuthal and zenithal perturbations from the
preferred (easy) alignment direction. The first term is necessary
to maintain the surface order parameter, Implementation [3]The implementation is well suited to the modelling of defect movement in realistically sized geometries, via the following features:
This implicit scheme leads to a larger memory use than the constant order program. However, the rapid spatial variations in the order parameter near disclinations severely limits the time step for explicit methods (<1ns!). We prefer the implicit method in this case to achieve reasonable simulation times. Flow of the liquid crystal is calculated by solving the Navier-Stokes equations with a stress tensor that takes into account the anisotropy of the LC. The following assumptions are made:
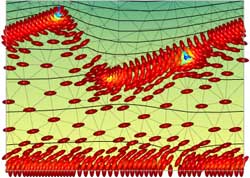
These assumptions could be dropped if required, at the cost of an increase in simultion time. The 2D and 3D implementations differ. In 2D second order shape functions are used for the Q-tensor, velocity and electric potential. A mixed interpolation is used for the Navier-Stokes equation to avoid oscillatory pressure solutions. Therefore first order shape functions are used for the pressure. In 3D first order shape functions are used for all variables, and a stabilized form of the Navier-Stokes equations. ResultsFig. 1 shows an example simultion results for a type of bistable display device.
Fig. 1: Defect movement in a Zenithally Bistable Nematic (ZBN) style device, with a negative dielectric anisotropy liquid crystal (director colour represents the order parameter)
[1] T. Qian and P. Sheng, “Generalized hydrodynamic equations
for nematic liquid [2] E. Willman, F. A. Fern´andez, R. James, and S. E. Day,
“Phenomenological [3] R. James, E. Willman, F. A. Fernandez, and S. E. Day, “Finite-element
modeling This page last modified 8 July, 2007 by r.james |

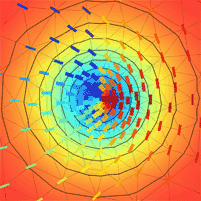 When disclinations are present, the LC ordering
becomes biaxial near the core and the order parameter drops (as
represented by the background colour of the figure to the right).
We have developed Finite Element discretisations of the Qian-Sheng
Equations in both 2D and 3D. The Qian-Sheng equations are a generalisation
of Ericksen-Leslie theory for LC hydrodynamics to include changes
in the order parameter [1]. The Finite Element Method is well suited
to resolve the rapid variations in order parameter about disclination
whilst still being able to model large container sizes.
When disclinations are present, the LC ordering
becomes biaxial near the core and the order parameter drops (as
represented by the background colour of the figure to the right).
We have developed Finite Element discretisations of the Qian-Sheng
Equations in both 2D and 3D. The Qian-Sheng equations are a generalisation
of Ericksen-Leslie theory for LC hydrodynamics to include changes
in the order parameter [1]. The Finite Element Method is well suited
to resolve the rapid variations in order parameter about disclination
whilst still being able to model large container sizes.