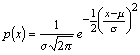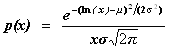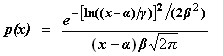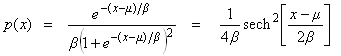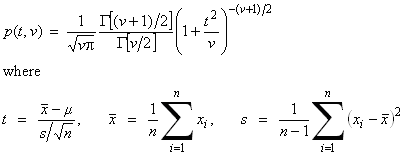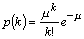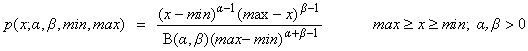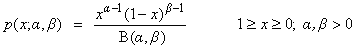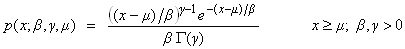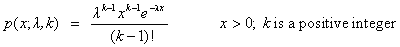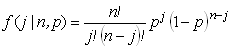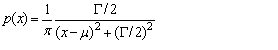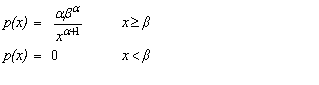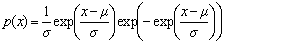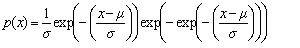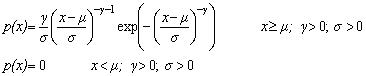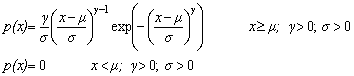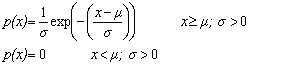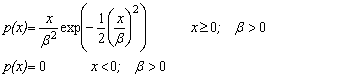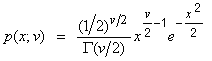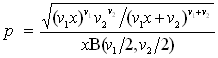|
|
|
| import statement: |
import flanagan.math.PsRandom; |
| Constructors | public void PsRandom() |
| public void PsRandom(long seed) | |
| Reset the seed | public void setSeed(long seed) |
| public long getSeed() | |
| public long getInitialSeed() | |
| Alter random number generators | public void setMethodDecimal(int option) |
| public int getMethodDecimal() | |
| public void setMethodInteger(int option) | |
| public int getMethodInteger() | |
| public void setMethodBinary(int option) | |
| public int getMethodBinary() | |
| Uniform deviates (floating point numbers) | public double nextDouble() |
| public double nextDouble(double rangeHigh) | |
| public double nextDouble(double rangeLow, double rangeHigh) | |
| public double[ ] doubleArray(int n) | |
| public double[ ] doubleArray(int n, double rangeHigh) | |
| public double[ ] doubleArray(int n, double rangeLow, double rangeHigh) | |
| Uniform deviates (integers) | public double nextInteger(int rangeHigh) |
| public double nextInteger(int rangeLow, int rangeHigh) | |
| public double[ ] integerArray(int n, int rangeHigh) | |
| public double[ ] integerArray(int n, int rangeLow, int rangeHigh) | |
| public double[ ] uniqueIntegerArray(int rangeHigh) | |
| public double[ ] uniqueIntegerArray(int rangeLow, int rangeHigh) | |
| Binary numbers [bits] | public int nextBit() |
| public int[ ] bitArray(int n) | |
| Gaussian (normal) deviates | public double nextGaussian() |
| public double nextGaussian(double mean, double sd) | |
| public double[ ] gaussianArray(double mean, double sd, int n) | |
| public double[ ][] correlatedGaussianArrays(double mean1, double mean2, double sd1, double sd2, double rho,int n) | |
| Beta distribution deviates | public double nextBeta(double min, double max, double alpha, double beta) |
| public double[ ] betaArray(double min, double max, double alpha, double beta, int n) | |
| public double nextBeta(double alpha, double beta) | |
| public double[ ] betaArray(double alpha, double beta, int n) | |
| Binomial deviates | public double nextBinomial(double prob, int nTrials) |
| public double binomialArray(double prob, int nTrials, int nArray) | |
| Chi-square deviates | public double nextChiSquare(int nu) |
| public double chiSquareArray(int nu, int nArray) | |
| Erlang distribution deviates | public double nextErlang(double lambda, int kay) |
| public double[ ] erlangArray(double lambda, int kay, int n) | |
| Exponential (Type 3 Extreme Value Distribution) deviates | public double nextExponential(double mu, double sigma) |
| public double[ ] exponentialArray(double mu, double sigma, int n) | |
| F-distribution deviates | public double nextF(int nu1, int nu2) |
| public double[ ] fArray(int nu1, int nu2, int n) | |
| Fréchet (Type 2 Extreme Value Distribution) deviates | public double nextFrechet(double mu, double sigma, double gamma) |
| public double[ ] frechetArray(double mu, double sigma, double gamma, int n) | |
| Gamma distribution deviates | public double nextGamma(double mu, double beta, double gamma) |
| public double[ ] gammaArray(double mu, double beta, double gamma, int n) | |
|
Gumbel (Type 1 Extreme Value Distribution) deviates (maximum order statistic) | public double nextMaximalGumbel(double mu, double sigma) |
| public double[ ] maximalGumbelArray(double mu, double sigma, int n) | |
|
Gumbel (Type 1 Extreme Value Distribution) deviates (minimum order statistic) | public double nextMinimalGumbel(double mu, double sigma) |
| public double[ ] minimalGumbelArray(double mu, double sigma, int n) | |
| Logistic distribution deviates | public double nextlogistic(double mu, double beta) |
| public double[ ] logisticArray(double mu, double beta, int n) | |
|
Log-normal distribution deviates (two parameter statistic) |
public double nextLogNormal(double mu, double sigma) public double nextLogNormalTwoPar(double mu, double sigma) |
|
public double[ ] logNormalArray(double mu, double sigma, int n) public double[ ] logNormalTwoParArray(double mu, double sigma, int n) | |
|
Log-normal distribution deviates (three parameter statistic) | public double nextLogNormalThreePar(double alpha, double beta, double gamma) |
| public double[ ] logNormalThreeParArray(double alpha, double beta, double gamma, int n) | |
| Lorentzian (Cauchy) deviates | public double nextLorentzian(double mu, double gamma) |
| public double[ ] lorentzianArray(double mu, double gamma, int n) | |
| Pareto deviates | public double nextPareto(double alpha, double beta, int n) |
| public double[ ] paretoArray(double alpha, double beta) | |
| Poissonian deviates | public double nextPoissonian(double mean) |
| public double[ ] poissonianArray(double mean, int n) | |
| Rayleigh (Type 3 Extreme Value Distribution) deviates | public double nextRayleigh(double beta) |
| public double[ ] rayleighArray(double beta, int n) | |
| Student's t-distribution deviates | public double nextStudentT(int nu) |
| public double[ ] studentTarray(int nu, int n) | |
| Weibull (Type 3 Extreme Value Distribution) deviates | public double nextWeibull(double mu, double sigma, double gamma) |
| public double[ ] weibullArray(double mu, double sigma, double gamma, int n) |