|
| INFORMATION FOR Prospective Students INFORMATION Home PROJECTS Funded QUICK LINKS Optical Devices
|
1D Matlab Liquid Crystal SolverThis page describes a simple Matlab based 1D solver to find the steady state liquid crystal orientation, using the Matlab Boundary Value Problem (BVP) solver, bvp4c. The theory and implementation is described using a one elastic constant formulation. A full three elastic constant formulation is available for download.
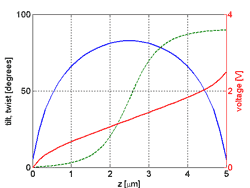
Fig. 1: Tilt, twist and voltage distributions in a twisted nematic (TN) cell
One Elastic Constant FormulationThe Oseen-Frank free energy may be written as
assuming there is no twist of the liquid crystal, where Taking first order variations we find that
This is a second order differential equation. To solve this using
the Matlab BVP solver, it must first be converted into two first
order equations by introducing an extra variable. Following the
approach shown here;
setting
Three Elastic Constant FormulationWith three elastic constants the free energy functional is supplemented
by terms that account for the splay-bend anisotropy of the liquid
crystal There are three elastic constants
The derivation, following the steps outlined in the previous section, is rather tedious. Instead one may use Maple to generate the equations. The Maple code can be downloaded here: lc3k.mws. I'm still learning Maple, so this code could be improved. This program solves for both the tilt and twist,
The function may be called as follows [z,theta,phi,u] = lc3k(volts); where z is a vector containing the locations of the mesh points, theta is the tilt, phi is the twist and u is the potential. It is assumed that a potential difference of volts is applied across the cell. Currently the material constants are hard coded into the function lc3k. Modify the program to take these as arguments if you wish. Currently the initial condition for the tilt is set to quadratic to improve convergence: In this latest version, alignment layers of finite thickness are supported. The left and right alignment layers may be of different thicknesses and relative permittivities. The thickness may also be set to zero. Anchoring may be strong or weak at the left and right alignment layers. Set W = Inf for strong anchoring. The anchoring energy is assumed isotropic and takes the form Fs = -W/2*(n.n0)^2. Warning: Since the implementation uses polar angles, it does not work well for large voltages as the twist becomes degenerate, leading to a singular Jacobian matrix. One way to avoid this problem is to discretise the equations in terms of the components of the director. A problem with this approach is that the unitary length of the director must in some way be enforced. This tends to increase the order of the governing equations and has a detrimental effect on the convergence. A simple Jones code calulates the optical transmittance. Finally, the Matlab code can be found here: lc3k.m. Dynamic FormulationAdditionally, a dynamic formulation, where the rate of change of the free energy is mediated by the rotational viscosity, gamma1, is available below. The solution is sought using the Matlab initial-boundary value solver for parabolic-elliptic PDEs, PDEPE. Weak anchoring and alignments layers are supported. This formulation is somewhat slower that the steady-state solver above. However, it is more stable, since it does not require the initial condition to be close to the desired solution. The Matlab code can be found here: lc3kdt.m.
This page last modified 16 April, 2010 by r.james |