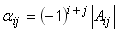|
Constructors
|
public Matrix(int nrow, int ncol)
|
|
|
public Matrix(int nrow, int ncol, double const)
|
|
|
public Matrix(double[][] twoD)
|
|
|
public Matrix(float[][] twoD)
|
|
|
public Matrix(long[][] twoD)
|
|
|
public Matrix(int[][] twoD)
|
|
|
public Matrix(BigDecimal[][] twoD)
|
|
|
public Matrix(BigInteger[][] twoD)
|
|
|
public Matrix(ArrayList<Object>[] twoD)
|
|
|
public Matrix(Vector<Object>[] twoD)
|
|
|
public Matrix(ArrayMaths[] twoD)
|
|
|
public Matrix(Matrix matrix)
|
|
|
Create Special Matrices
|
public void setIdentityMatrix()
|
public static Matrix identityMatrix(int nrow)
|
|
public void setUnitMatrix()
|
public static Matrix unitMatrix(int nrow, int ncol)
|
|
|
public static Matrix unitMatrix(int nrow, int ncol, int ncol)
|
public void setScalarMatrix(double diagconst)
|
public static Matrix scalarMatrix(int nrow,
double diagconst)
|
|
|
public static Matrix scalarMatrix(int nrow, int ncol,
double diagconst)
|
public void setDiagonalMatrix(double[] diag)
|
public static Matrix diagonalMatrix(int nrow, double[] diag)
|
|
|
public static Matrix diagonalMatrix(int nrow, int ncol, double[] diag)
|
|
Row Matrix
|
|
public static Matrix rowMatrix(double[] oneDarray)
|
|
Column Matrix
|
|
public static Matrix columnMatrix(double[] oneDarray)
|
|
Set values
|
public void setTwoDarray(double[][] twoD)
|
|
|
public void setElement(int i, int j, double aa)
|
|
|
public void setSubMatrix(int i, int j, double[][] submat)
|
|
|
public void setSubMatrix(int i, int j, int k, int l, double[][] submat)
|
|
|
public void setSubMatrix(int[] row, int[] col, double[][] submat)
|
|
|
Get values
|
public int getNrow()
|
|
|
public int getNcol()
|
|
|
public double[][] getArrayReference()
|
|
|
public double[][] getArrayCopy()
|
|
|
public double[] getRowCopy(int i)
|
|
|
public double[] getColumnCopy(int i)
|
|
|
public double getElement(int i, int j)
|
|
|
public Matrix getSubMatrix(int i, int j, int k, int l)
|
|
|
public Matrix getSubMatrix(int[] row, int[] col)
|
|
|
public int[] getIndexReference()
|
|
|
public int[] getIndexCopy()
|
|
|
public double getSwap()
|
|
|
Deep Copy
|
public Matrix copy()
|
public static Matrix copy(Matrix aa)
|
|
public Object clone()
|
|
|
Addition
|
public Matrix plus(Matrix bb)
|
public static Matrix plus(Matrix aa, Matrix bb)
|
|
public Matrix plus(double[][] bb)
|
|
|
public void plusEquals(Matrix bb)
|
|
|
Subtraction
|
public Matrix minus(Matrix bb)
|
public static Matrix minus(Matrix aa, Matrix bb)
|
|
public Matrix minus(double[][] bb)
|
|
|
public void minusEquals(Matrix bb)
|
|
|
Multiplication
|
public Matrix timesRightSideMatrix(Matrix bb)
|
public static Matrix timesMatrix(Matrix aa, Matrix bb)
|
|
public Matrix timesRightSideMatrix(double[][] bb)
|
public static Matrix timesMatrix(Matrix aa, double[][] bb)
|
|
public Matrix timesLeftSideMatrix(Matrix bb)
|
|
|
public Matrix timesLeftSideMatrix(double[][] bb)
|
public static Matrix timesMatrix(double[][] bb, Matrix aa)
|
|
public double[] timesRightSideColumnVector(double[] vec)
|
public static double[] timesRightSideColumnVector(Matrix aa, double[] vec)
|
|
public Matrix timesLeftSideColumnVector(double[] vec)
|
public static Matrix timesLeftSideColumnVector(double[] bb, Matrix aa)
|
|
public Matrix timesRightSideRowVector(double[] vec)
|
public static Matrix timesRightSideRowVector(Matrix aa, double[] vec)
|
|
public double[] timesLeftSideRowVector(double[] vec)
|
public static double[] timesLeftSideRowVector(double[] bb, Matrix aa)
|
|
public Matrix timesConstant(double bb)
|
public static Matrix timesConstant(Matrix aa, double bb)
|
|
public void timesRightSideMatrixEquals(Matrix bb)
|
|
public void timesRightSideMatrixEquals(double[][] bb)
|
|
|
public void timesLeftSideMatrixEquals(Matrix bb)
|
|
public void timesLeftSideMatrixEquals(double[][] bb)
|
|
|
public void timesConstantEquals(double bb)
|
|
|
|
Division
|
public Matrix over(Matrix bb)
|
public static Matrix over(Matrix aa, Matrix bb)
|
|
public Matrix over(double[][] bb)
|
public static Matrix over(Matrix aa, double[][] bb)
|
|
|
public static Matrix over(double[][] aa, double[][] bb)
|
|
public void overEquals(Matrix bb)
|
|
|
public void overEquals(double[][] bb)
|
|
|
|
Inverse
|
public Matrix inverse()
|
public static Matrix inverse(Matrix aa)
|
|
Transpose
|
public Matrix transpose()
|
public static Matrix transpose(Matrix aa)
|
|
Opposite
|
public Matrix opposite()
|
public static Matrix opposite(Matrix aa)
|
|
Reduced Row Echelon Form
|
public Matrix reducedRowEchelonForm()
|
|
|
Hessenberg matrix
|
public double[][] getHessenbergMatrix()
|
|
|
Trace
|
public double trace()
|
public static double trace(Matrix aa)
|
|
Determinant
|
public double determinant()
|
public static double determinant(Matrix aa)
|
|
|
public static double determinant(double[][] aa)
|
|
public double logDeterminant()
|
public static double logDeterminant(Matrix aa)
|
|
|
public static double logDeterminant(double[][] aa)
|
|
Cofactor
|
public Matrix cofactor()
|
|
|
public double cofactor(int i, int j)
|
|
|
Norms
|
public double frobeniusNorm()
|
|
|
public double oneNorm()
|
|
|
public double infinityNorm()
|
|
|
Eigenvalues and eigenvectors
|
public double[] getEigenValues()
|
|
public double[] getSortedEigenValues()
|
|
public double[][] getEigenVectorsAsRows()
|
# |
public double[][] getEigenVectorsAsColumns()
|
|
public double[][] getSortedEigenVectorsAsRows()
|
|
public double[][] getSortedEigenVectorsAsColumns()
|
|
public int[][] eigenValueIndices()
|
|
public int getNumberOfJacobiRotations()
|
|
|
LU Decompostion
|
public Matrix luDecomp()
|
|
|
public double luBackSub(double[] bvec)
|
|
|
public void resetLUzero(double luZero)
|
|
|
Linear Equation Set
|
public double[] solveLinearSet(double[] bvec)
|
|
|
Pivot
|
public int[] pivot()
|
|
|
Maximum element
|
public double[] maximumElement()
|
|
|
public double[] rowMaxima()
|
|
|
public double[] columnMaxima()
|
|
|
Minimum element
|
public double[] minimumElement()
|
|
|
public double[] rowMinima()
|
|
|
public double[] columnMinima()
|
|
|
Range
|
public double range()
|
|
|
public double[] rowRanges()
|
|
|
public double[] columnRanges()
|
|
|
Sum of elements
|
public double sum()
|
|
|
public double[] rowSums()
|
|
|
public double[] columnSums()
|
|
|
Mean of elements
|
public double mean()
|
|
|
public double[] rowMeans()
|
|
|
public double[] columnMeans()
|
|
|
Subtract the mean of elements
|
public Matrix subtractMean()
|
|
|
public Matrix subtractRowMeans()
|
|
|
public Matrix subtractColumnMeans()
|
|
|
Median of elements
|
public double median()
|
|
|
public double[] rowMedians()
|
|
|
public double[] columnMedians()
|
|
|
Set variance denominator et al.
|
public void setDenominatorToN()
|
|
|
Variance of elements
|
public double variance()
|
|
|
public double[] rowVariances()
|
|
|
public double[] columnVariances()
|
|
|
Standard deviation of elements
|
public double standardDeviation()
|
|
|
public double[] rowStandardDeviations()
|
|
|
public double[] columnStandardDeviations()
|
|
|
Standard error of elements
|
public double standardError()
|
|
|
public double[] rowStandardErrors()
|
|
|
public double[] columnStandardErrors()
|
|
|
Logical tests
|
public boolean isSquare()
|
|
public boolean isSymmetric()
|
public boolean isNearlySymmetric(double tolerance)
|
public boolean isIdentity()
|
public boolean isNearlyIdentity(double tolerance)
|
public boolean isUnit()
|
public boolean isNearlyUnit(double tolerance)
|
public boolean isZero()
|
public boolean isNearlyZero(double tolerance)
|
public boolean isDiagonal()
|
public boolean isNearlyDiagonal(double tolerance)
|
public boolean isLowerTriagonal()
|
public boolean isNearlyLowerTriagonal(double tolerance)
|
public boolean isUpperTriagonal()
|
public boolean isNearlyUpperTriagonal(double tolerance)
|
public boolean isTridiagonal()
|
public boolean isNearlyTridiagonal(double tolerance)
|
public boolean isLowerHessenberg()
|
public boolean isNearlyLowerHessenberg(double tolerance)
|
public boolean isUpperHessenberg()
|
public boolean isNearlyUpperHessenberg(double tolerance)
|
public boolean isSingular()
|
public boolean isNearlySingular(double tolerance)
|
public ArrayList<Integer> identicalRows()
|
public ArrayList<Integer> identicalColumns()
|
public ArrayList<Integer> zeroRows()
|
public ArrayList<Integer> zeroColumns()
|