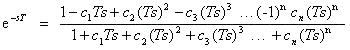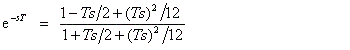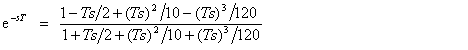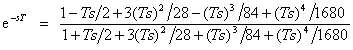Michael Thomas Flanagan's Java Scientific Library

ZeroOrderHold Class:     Modelling a Zero Order Hold for Control Theory Simulations

      

Last update: 8 November 2009                                                                                                                              Main Page of Michael Thomas Flanagan's Java Scientific Library

This class contains the constructor to create an instance of a zero order hold (ZOH) and the methods needed to use this ZOH in control loops in the time domain, Laplace transform s domain or the z-transform z domain.
The ZOH s-domain transfer function is (1 - exp(-Ths))/s where Th is the hold time. The Pade approximation is used in s-domain (1 to 4 order Pade approximations are available)

This is a subclass of the superclass BlackBox

import directive: import flanagan.control.ZeroOrderHold;

SUMMARY OF CONSTRUCTORS AND METHODS

METHODS FOUND ONLY IN THE SUBCLASS ZeroOrderHold

Constructors   public ZeroOrderHold(double holdTime)
  public ZeroOrderHold(double holdTime, double padeOrder)

METHODS INHERITED FROM THE SUPERCLASS BlackBox

Deep Copy   public ZeroOrderHold copy()
Overridden
public Object clone()
Overridden
s-domain transfer function Get the numerator degree public int getSnumerDeg()
Not overridden
Get the numerator polynomial public ComplexPoly getSnumer()
Not overridden
Get the denominator degree public int getSdenomDeg()
Not overridden
Get the denominator polynomial public ComplexPoly getSdenom()
Not overridden
Get the s-values of the poles publicComplex[ ] getPolesS()
Not overridden
Get the s-values of the zeros publicComplex[ ] getZerosS()
Not overridden
Plot poles and zeros public void plotPolesZeroS()
Not overridden
Set the value of the Laplace s variable public void setS(Complex sValue)
Not overridden
public void setS(double sReal, double sImag)
Not overridden
public void setS(double sImag)
Not overridden
Get the Laplace s value public Complex getS()
Not overridden
Evaluate transfer function public Complex evalTransFunctS()
Not overridden
public Complex evalTransFunctS(Complex sValue)
Not overridden
public Complex evalTransFunctS(double freq)
Not overridden
Evaluate transfer function magnitude public double evalMagTransFunctS()
Not overridden
public double evalMagTransFunctS(Complex sValue)
Not overridden
public double evalMagTransFunctS(double freq)
Not overridden
Evaluate transfer function phase public double evalPhaseTransFunctS()
Not overridden
public double evalPhaseTransFunctS(Complex sValue)
Not overridden
public double evalPhaseTransFunctS(double freq)
Not overridden
Bode plots (magnitude and phase) public void plotBode(double lowFreq, double highFreq,)
Not overridden
Inverse Laplace Transform public static Complex[ ] [ ] inverseTransform(ComplexPoly numer, ComplexPoly Not overridden
public static Complex timeTerm(double time, Complex coeff, Complex constant, Complex power)
Not overridden
Set the input in the s-domain public void setInputS(Complex input)
Not overridden
Get the input in the s-domain public Complex getInputS()
Not overridden
Get the output in the s-domain public Complex getOutputS()
Not overridden
public Complex getOutputS(Complex sValue, Complex input)
Not overridden
Pade
Approximation 		Set the Pade order public void setPadeOrder(double padeorder)
Not overridden
Get the Pade order public void setPadeOrder(double padeorder)
Not overridden
Continuous time domain
(uses the s-domain transfer function) 		Plot step input transient public void stepInput(double finaltime)
Not overridden
public void stepInput(double mag, double finaltime)
Not overridden
Plot ramp input transient public void rampInput(double finaltime)
Not overridden
public void rampInput(double mag, double finaltime)
Not overridden
public void rampInput(int order, double finaltime)
Not overridden
public void rampInput(double mag, int order, double finaltime)
Not overridden
z-domain transfer function Map s-transfer function into the z-domain public void zTransform()
Not overridden
public void zTransform(double deltaT)
Not overridden
Get the numerator degree public int getZnumerDeg()
Not overridden
Get the numerator polynomial public ComplexPoly getZnumer()
Not overridden
Get the denominator degree public int getZdenomDeg()
Not overridden
Get the denominator polynomial public ComplexPoly getZdenom()
Not overridden
Get the z-values of the poles publicComplex[ ] getPolesZ()
Not overridden
Get the z-values of the zeros publicComplex[ ] getZerosZ()
Not overridden
Plot poles and zeros public void plotPolesZeroZ()
Not overridden
Set the value of the z variable public void setZ(Complex zValue)
Not overridden
public void setZ(double zReal, double zImag)
Not overridden
Get the z value public Complex getZ()
Not overridden
Evaluate transfer function public Complex evalTransFunctZ()
Not overridden
public Complex evalTransFunctZ(Complex zValue)
Not overridden
Evaluate transfer function magnitude public double evalMagTransFunctZ()
Not overridden
public double evalMagTransFunctZ(Complex zValue)
Not overridden
Evaluate transfer function phase public double evalPhaseTransFunctZ()
Not overridden
public double evalPhaseTransFunctZ(Complex zValue)
Not overridden
Sampled signal Set the sampling length public void setSampleLdength(int samplelength)
Not overridden
Get the sampling length public int getSampleLength()
Not overridden
Set the sampling period public void setDeltaT(double deltaT)
Not overridden
Get the sampling period public double getDeltaT()
Not overridden
Set the sampling frequency public void setSampFreq(double sfreq)
Not overridden
Get the sampling frequency public double getSampFreq()
Not overridden
Set the sampled input and time public void setInputT(double time, double input)
Not overridden
Get the current value of the time public double getCurrentTime()
Not overridden
Get the array of times public double[] getTime()
Not overridden
Get the current value of the input public double getCurrentInputT()
Not overridden
Get the array of the inputs public double[] getInputT()
Not overridden
Calculate the current value of the output public double calcOutputT()
Not overridden
public double calcOutputT(double time, double input) Not overridden
Get the current value of the output public double getCurrentOutputT()
Not overridden
Get the array of the outputs public double getOutputT()
Not overridden
Set numerical integration method public void setIntegrateMethod(int integMethod)
Not overridden
public void setIntegrateMethod(String integMethodOpt)
Not overridden
Get numerical integration method public int getIntegrateMethod()
Not overridden
General methods Reset all inputs, outputs and times to zero public void resetZero()
Not overridden
Set the name of the black box public void setName(String name)
Not overridden
Get the name of the black box public String getName()
Not overridden


CONSTRUCTORS

 public ZeroOrderHold(double holdTime)
public ZeroOrderHold(double holdTime, double padeOrder)
Usage:                      ZeroOrderHold delay = new ZeroOrderHold(holdTime);
This constructor creates a new instance of ZeroOrderHold with a hold time set to the argument, e.g. holdTime in the above usage. The hold time is stored as the superclass BlackBox data member that stores a dead time and is treated as a dead time by classes combining BlackBoxes, e.g. OpenPath, ClosedLoop.
Usage:                      ZeroOrderHold zoh = new ZeroOrderHold(holdTime, padeOrder);
This constructor creates a new instance of ZeroOrderHold with a hold time set to the argument, e.g. holdTime in the above usage, and resets the order of the Pade approximation used to represent the Laplace Transform of exp(Ths. The hold time is stored as the superclass BlackBox data member that stores a dead time and is treated as a dead time by classes combining BlackBoxes, e.g. OpenPath, ClosedLoop.
The Laplace transform of a hold time, T, is exp(-sT). The Pade approximation, of order, n, is the is given by:

The argument of this method, padeOrder, in the above usage, is the order, n. This method supports orders between 1 and 4. If a value below 1 is enterted a order of 1 is used. If a value above 4 is entered a order of 4 is used. The default value, i.e. the order used if this method is not invoked, is 2.
The approximations are:
First order

Second order (default approximation)

Third order

Fourth order



OTHER CLASSES USED BY THIS CLASS

 This class is a subclass of BlackBox which uses the following classes in this library:

This page was prepared by Dr Michael Thomas Flanagan