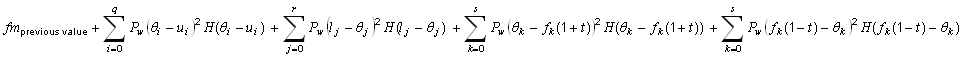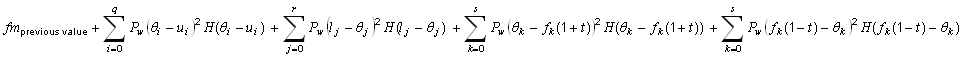|
Constructors
|
|
public Maximization()
|
|
public Maximisation()
|
|
Maximisation
|
Nelder and Mead Simplex
for y = f(a[0],a[1],a[2]...)
|
public void nelderMead(MaximizationFunction mf, double[ ] start, double[ ] step, double ftol, int nmax)
|
|
public void nelderMead(MaximisationFunction mf, double[ ] start, double[ ] step, double ftol, int nmax)
|
|
public void nelderMead(MaximizationFunction mf, double[ ] start, double[ ] step, double ftol)
|
|
public void nelderMead(MaximisationFunction mf, double[ ] start, double[ ] step, double ftol)
|
|
public void nelderMead(MaximizationFunction mf, double[ ] start, double[ ] step, int nmax)
|
|
public void nelderMead(MaximisationFunction mf, double[ ] start, double[ ] step, int nmax)
|
|
public void nelderMead(MaximizationFunction mf, double[ ] start, double ftol, int nmax)
|
|
public void nelderMead(MaximisationFunction mf, double[ ] start, double ftol, int nmax)
|
|
public void nelderMead(MaximizationFunction mf, double[ ] start, double[ ] step)
|
|
public void nelderMead(MaximisationFunction mf, double[ ] start, double[ ] step)
|
|
public void nelderMead(MaximizationFunction mf, double[ ] start, double ftol)
|
|
public void nelderMead(MaximisationFunction mf, double[ ] start, double ftol)
|
|
public void nelderMead(MaximizationFunction mf, double[ ] start, int nmax)
|
|
public void nelderMead(MaximisationFunction mf, double[ ] start, int nmax)
|
|
public void nelderMead(MaximizationFunction mf, double[ ] start)
|
|
public void nelderMead(MaximisationFunction mf, double[ ] start)
|
|
Constrained maximization
|
public void addConstraint(int pIndex, int direction, double boundary)
|
|
public void addConstraint(int[] pIndices, double[] plusOrMinus, int direction, double boundary)
|
|
public void addConstraint(int[] pIndices, int[] plusOrMinus, int direction, double boundary)
|
|
public void removeConstraints()
|
|
public void setPenaltyWeight(double pWeight)
|
|
public double getPenaltyWeight()
|
|
public void setConstraintTolerance(double tolerance)
|
|
Scaling the initial estimates
|
public void setScale(int opt)
|
|
public void setScale(double[] opt)
|
|
public double[ ] getScale()
|
|
Convergence tests
|
public boolean getConvStatus()
|
|
public void setTolerance(double tol)
|
|
public int getTolerance()
|
|
public double getSimplexSd()
|
|
Restarts
|
public void setNrestartsMax(int nrm)
|
|
public int getNrestartsMax()
|
|
public int getNrestarts()
|
|
Number of iterations
|
public void setNmax(int nMax)
|
|
public int getNmax()
|
|
public int getNiter()
|
|
Nelder and Mead Simplex Coefficients
|
public void setNMreflect(double reflectC)
|
|
public double getNMreflect()
|
|
public void setNMextend(double extendC)
|
|
public double getNMextend()
|
|
public void setNMcontract(double contractC)
|
|
public double getNMcontract()
|
|
Print the maximization results
|
public void print( String filename, int prec)
|
|
public void print( String filename)
|
|
public void print(int prec)
|
|
public void print()
|
|
Return the parameter values, a[i], at maximum
|
public double[] getParamValues()
|
|
Return the function value at maximum
|
public double getMaximum()
|
|
Suppress message
|
public void suppressNoConvergenceMessage()
|