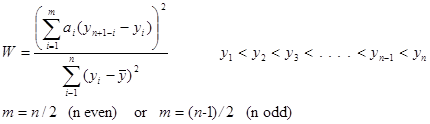Usage: coeff = norm.shapiroWilkCoeff(nPoints);
This method returns the Shapiro-Wilk coefficients for n points where n is entered as the argument nPoints.
NORMAL PROBABILITY PLOTS (GAUSSIAN PROBABILITY PLOTS)
This section describes methods for plotting and analysising Normal Probability Plots where the Normal probability density function is defined as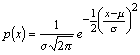
Naming note: normal may be replaced by gaussian in the names of all these methods, e.g. gaussianProbabilityPlot() performs the same function as normalProbabilityPlot()
Calculate and Display a Normal Probabilty Plot
public void normalProbabilityPlot()
Usage: norm.normalProbabilityPlot();
This method calculates and displays a Normal probablity plot, i.e. a plot of the data entered via the Constructor (ordinate) against the corresponding Normal order statistic medians (abscissa), and the best fit straight line. The data is first sorted into an ascending order.
User supplied initial estimates
public void normalUserSuppliedInitialEstimates(double mu, double sigma)
Usage: norm.normalUserSuppliedInitialEstimates(mu, sigma);
This method allows the user to override the above method's [normalProbabilityPlot()] automatic calculation of the initial estimates of μ and σ and enter their own initial estimates of μ [mu] and σ [sigma]. If this method is required it must be called before normalProbabilityPlot() is called. See the warning note 1 for an explanation of the possible need for this method.
Remove user supplied initial estimates
public void removeNormalUserSuppliedInitialEstimates()
Usage: norm.removeNormalUserSuppliedInitialEstimates();
This method removes initial estimates supplied by the user via the method normalUserSuppliedInitialEstimates(mu, sigma) [see immediately above]. The automatic calculation of the initial estimates of μ and σ by normalProbabilityPlot() is restored on calling this method.
Return the Correlation Coefficient
public double normalCorrelationCoefficient()
Usage: rho = norm.normalCorrelationCoefficient();
This method returns the correlation coefficient of the data entered via the Constructor and the corresponding Normal order statistic medians. The data is first sorted into an ascending order.
Return the Gradient
public double normalGradient()
Usage: gradient = norm.normalGradient();
This method returns the gradient of the best straight line fit to the Normal probability plot, i.e. a plot of the data entered via the Constructor (ordinate) against the corresponding Normal order statistic medians (abscissa). The data is first sorted into an ascending order.
Return the Estimated Error of the Gradient
public double normalGradientError()
Usage: gradientError = norm.normalGradientError();
This method returns the estimated error of the gradient of the best straight line fit to the Normal probability plot, i.e. a plot of the data entered via the Constructor (ordinate) against the corresponding Normal order statistic medians (abscissa). The data is first sorted into an ascending order. The error is obtained from the linear regression.
Return the Intercept
public double normalIntercept()
Usage: intercept = norm.normalIntercept();
This method returns the intercept of the best straight line fit to the Normal probability plot, i.e. a plot of the data entered via the Constructor (ordinate) against the corresponding Normal order statistic medians (abscissa). The data is first sorted into an ascending order.
Return the Estimated Error of the Intercept
public double normalInterceptError()
Usage: interceptError = norm.normalInterceptError();
This method returns the estimated error of the intercept of the best straight line fit to the Normal probability plot, i.e. a plot of the data entered via the Constructor (ordinate) against the corresponding Normal order statistic medians (abscissa). The data is first sorted into an ascending order. The error is obtained from the linear regression.
Return normal parameter μ
public double normalMu()
Usage: mu = norm.normalMu();
This method returns the Normal parameter, μ, obtained from the best fit Probabilty Plot calculated as the one with the minimum sum of squares of the diferences in the data values entered via the Constructor and the corresponding Normal order statistic median value. The data is first sorted into an ascending order. See also Warning.
Return the Estimated Error of the normal parameter μ
public double normalMuError()
Usage: muError = norm.normalMuError();
This method returns the estimated error of the Normal parameter, μ. The error is obtained as the square root of the appropriate diagonal of a covariance matrix obtained as the inverse of the numerically calculated matrix of second derivatives of the sum of squares with respect to μ and σ. See also Warning.
Return normal parameter σ
public double normalSigma()
Usage: sigma = norm.normalSigma();
This method returns the Normal parameter, σ, obtained from the best fit Probabilty Plot calculated as the one with the minimum sum of squares of the diferences in the data values entered via the Constructor and the corresponding Normal order statistic median value. The data is first sorted into an ascending order. See also Warning.
Return the Estimated Error of the normal parameter σ
public double normalSigmaError()
Usage: sigmaError = norm.normalSigmaError();
This method returns the estimated error of the Normal parameter, σ. The error is obtained as the square root of the appropriate diagonal of a covariance matrix obtained as the inverse of the numerically calculated matrix of second derivatives of the sum of squares with respect to μ and σ. See also Warning.
Return the Sum of Squares
public double normalSumOfSquares()
Usage: ss = norm.normalSumOfSquares();
This method returns the unweighted sum of squares of the diferences in the data values entered via the unweighted regression Constructor and the corresponding Normal order statistic median value. The data is first sorted into an ascending order.
Return the Normal Order Statistic Medians
public double[] normalOrderStatisticMedians()
Usage: gsom = norm.normalOrderStatisticMedians();
This method returns the Normal order statistic median used in the Probability Plot.
STANDARD NORMAL PROBABILITY PLOT
See above for the Two Parameter Normal Standard Probability Plot
This section describes methods for plotting and analysising Standard Normal Probability Plots where the Standard Normal probabilty density function is defined as
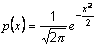
Naming note: normalStandard may be replaced by gaussianStandard in the names of all these methods, e.g. gaussianStandardProbabilityPlot() performs the same function as normalStandardProbabilityPlot().
Calculate and Display a Standard Normal Probabilty Plot
public void normalStandardProbabilityPlot()
Usage: norm.normalStandardProbabilityPlot();
This method calculates and displays a Standard Normal probablity plot, i.e. a plot of the data entered via the Constructor (ordinate) against the corresponding Standard Normal order statistic medians (abscissa), and the best fit straight line. The data is first sorted into an ascending order.
Return the Correlation Coefficient
public double normalStandardCorrelationCoefficient()
Usage: rho = norm.normalStandardCorrelationCoefficient();
This method returns the correlation coefficient of the data entered via the Constructor and the corresponding Standard Normal order statistic medians. The data is first sorted into an ascending order.
Return the Gradient
public double normalStandardGradient()
Usage: gradient = norm.normalStandardGradient();
This method returns the gradient of the best straight line fit to the Standard Normal probability plot, i.e. a plot of the data entered via the Constructor (ordinate) against the corresponding Standard Normal order statistic medians (abscissa). The data is first sorted into an ascending order.
Return the Estimated Error of the Gradient
public double normalStandardGradientError()
Usage: gradientError = norm.normalStandardGradientError();
This method returns the estimated error of the gradient of the best straight line fit to the Standard Normal probability plot, i.e. a plot of the data entered via the Constructor (ordinate) against the corresponding Standard Normal order statistic medians (abscissa). The data is first sorted into an ascending order. The error is obtained from the linear regression.
Return the Intercept
public double normalStandardIntercept()
Usage: intercept = norm.normalStandardIntercept();
This method returns the intercept of the best straight line fit to the Standard Normal probability plot, i.e. a plot of the data entered via the Constructor (ordinate) against the corresponding Standard Normal order statistic medians (abscissa). The data is first sorted into an ascending order.
Return the Estimated Error of the Intercept
public double normalStandardInterceptError()
Usage: interceptError = norm.normalStandardInterceptError();
This method returns the estimated error of the intercept of the best straight line fit to the Standard Normal probability plot, i.e. a plot of the data entered via the Constructor (ordinate) against the corresponding Standard Normal order statistic medians (abscissa). The data is first sorted into an ascending order. The error is obtained from the linear regression.
Return the Sum of Squares
public double normalStandardSumOfSquares()
Usage: ss = norm.normalStandardSumOfSquares();
This method returns the sum of squares of the diferences in the data values entered via the unweighted regression Constructor and the corresponding Standard Normal order statistic median value. The data is first sorted into an ascending order.
Return the Standard normalStandard Order Statistic Medians
public double[] normalStandardOrderStatisticMedians()
Usage: gsom = norm.normalStandardOrderStatisticMedians();
This method returns the Standard Normal order statistic median used in the Probability Plot.
DATA
Original data
public double[] getData()
Usage: data = norm.getData();
This method returns the entered data as a double[] array in the order in which the data was entered.
Ordered data
public double[] getOrderedData()
Usage: orddata = norm.getOrderedData();
This method returns the entered data as a double[] array sorted into ascending oder.
OTHER CLASSES USED BY THIS CLASS
This class uses the following classes in this library:PERMISSION TO USE
Permission to use, copy and modify this software and its documentation for NON-COMMERCIAL purposes is granted, without fee, provided that an acknowledgement to the author, Dr Michael Thomas Flanagan at www.ee.ucl.ac.uk/~mflanaga, appears in all copies and associated documentation or publications.
Public listing of the source codes on the internet is not permitted.
Redistribution of the source codes or of the flanagan.jar file is not permitted.
Redistribution in binary form of all or parts of these classes is not permitted.
Dr Michael Thomas Flanagan makes no representations about the suitability or fitness of the software for any or for a particular purpose. Dr Michael Thomas Flanagan shall not be liable for any damages suffered as a result of using, modifying or distributing this software or its derivatives.
This page was prepared by Dr Michael Thomas Flanagan