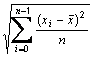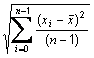Set the precision with which floating point numbers are written
public void numberOfDecimalPlaces(int trunc)
Usage: pca.numberOfDecimalPlaces(trunc)
This optional method sets the number of places displayed after the decimal point when floating point numbers are written to an output file. The number of places required is entered via the argument trunc. The default value is 6. The displayed number is the rounded equivalent of the stored number. If the precision of the entered data is greater than the value trunc the output method overides the trunc value and uses the maximum precision of the entered data. See immediately below (numberOfDecimalPlacesAll) for a method that sets the output precision irrespective of the input precision.
public void numberOfDecimalPlacesAll(int trunc)
Usage: pca.numberOfDecimalPlacesAll(trunc)
This optional method sets the number of places displayed after the decimal point when floating point numbers are written to an output file. The number of places required is entered via the argument trunc. The default value is 6. The displayed number is the rounded equivalent of the stored number. The precision set by this method is used in the output irrespective of the precision of the input data. See immediately above (numberOfDecimalPlaces) for a method that sets takes the precision of the entered data into account.
SCREE PLOTS
Data and parallel analysis scree Plotpublic void screePlot()
Usage: pca.screePlot()
This method displays the following scree plots on one graph:
- Data eigenvalues
- Parallel analysis eigenvalue means with standard deviation error bars
- Parallel analysis eigenvalue percentiles
public void screePlotDataAlone()
Usage: pca.screePlotDataAlone()
This method displays the scree plot of the data eigenvalues only.
EIGENVALUES
DATA EIGENVALUESData eigenvalues as calculated
public double[] eigenValues()
Usage: eigenvalues = pca.eigenValues()
This method returns all the eigenvalues as calculated. See below for ordered eigenvalues.
Ordered data eigenvalues
public double[] orderedEigenValues()
Usage: eigenvalues = pca.orderedEigenValues()
This method returns all the eigenvalues sorted into a descending order.
Eigenvalue indices
public int[] eigenValueIndices()
Usage: indices = pca.eigenValueIndices()
This method returns the indices of the eigenvalues before they were sorted into a descending order.
Eigenvalue proportions as a percentage
public double[] proportionPercentage()
Usage: prop = pca.proportionPercentage()
This method returns the eigenvalues sorted into a descending order and expressed as a percentage of the total of all the eigenvalues.
Eigenvalue proportions as a cumulative percentage
public double[] cumulativePercentage()
Usage: cumul = pca.cumulativePercentage()
This method returns the eigenvalues sorted into a descending order and expressed as a cumulative percentage of the total of all the eigenvalues.
PARALLEL ANALYSIS EIGENVALUES
Eigenvalues from all simulations
public double[][] monteCarloEigenValues()
Usage: simuleigenvalues = pca.monteCarloEigenValues()
This method returns all the eigenvalues for all the simulations. Each row contains the eigenvalues, in descending order, for an individual simulation.
Means of the ordered eigenvalues from all simulations
public double[] monteCarloEigenMeans()
Usage: simulmeans = pca.monteCarloEigenMeans()
This method returns the means of the ordered eigenvalues for all the simulations.
Standard deviations of the ordered eigenvalues from all simulations
public double[] monteCarloEigenStandardDeviations()
Usage: simulsds = pca.monteCarloEigenStandardDeviations()
This method returns the standard deviations of the ordered eigenvalues for all the simulations.
Percentiles of the ordered eigenvalues from all simulations
public double[] monteCarloEigenPercentiles()
Usage: simulpc = pca.monteCarloEigenPercentiles()
This method returns the percentiless of the ordered eigenvalues for all the simulations. The default value percenyile is a 95% percentile. See percentile value for restting the percentile value.
NUMBER OF SIGNIFICANT COMPONENTS
public int nOneOrGreater()public int nMeanCrossover()
public int nPercentileCrossover()
Usage: nSignificant = pca.nOneOrGreater()
This method returns the number of unrotated eigenvalues with values greater than or equal to unity.
Usage: nSignificant = pca.nMeanCrossover()
This method returns the number of unrotated eigenvalues with values greater than the corresponding means of the eigenvalues obtained from the Monte Carlo simulations using random data sets.
Usage: nSignificant = pca.nPercentileCrossover()
This method returns the number of unrotated eigenvalues with values greater than the corresponding percentiles of the eigenvalues obtained from the Monte Carlo simulations using random data sets. The default percentile is a 95% percentile. See set percentile for a method that resets the percentile to a user supplied value.
EIGENVECTORS
DATA EIGENVECTORSData eigenvectors as calculated
public double[][] eigenVectorsAsRows()
public double[][] eigenVectorsAsColumns()
Usage: eigenvectors = pca.eigenVectorsAsRows()
This method returns all the eigenvectors as calculated with each eigenvector corresponding to an eigenvalue returned as a row. See below for ordered eigenvectors.
Usage: eigenvectors = pca.eigenVectorsAsColumns()
This method returns all the eigenvectors as calculated with each eigenvector corresponding to an eigenvalue returned as a column. See below for ordered eigenvectors.
Ordered data eigenvectors
public double[][] orderedEigenVectorAsRows()
public double[][] orderedEigenVectorAsColumns()
Usage: eigenvectors = pca.orderedEigenVectorsAsRows()
This method returns all the eigenvectors sorted to match a descending order of the corresponding eigenvalues. Each eigenvector corresponding to an eigenvalue returned as a row.
Usage: eigenvectors = pca.orderedEigenVectorsAsColumnss()
This method returns all the eigenvectors sorted to match a descending order of the corresponding eigenvalues. Each eigenvector corresponding to an eigenvalue returned as a column.
LOADING FACTORS
public double[][] loadingFactorsAsRows()public double[][] loadingFactorsAsColumns()
Usage: loadingFactors = pca.loadingFactorsAsRows()
This method returns all the loading factors with loading factors corresponding to an eigenvalue returned as a row. Loading factors are calculated by multiplying the corresponding eigenvector by the square root of the relevant eigenvalue.
Usage: eigenvectors = pca.loadingFactorsAsColumns()
This method returns all the loading factors with loading factors corresponding to an eigenvalue returned as a column. Loading factors are calculated by multiplying the corresponding eigenvector by the square root of the relevant eigenvalue.
COMMUNALITIES
public double[] communalities()Usage: communalities = pca.communalities()
This method returns all the communalities, hi2, where
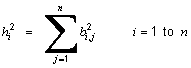
bi,j are the loading factors (as rows) and n is the number of items. The communality, h12, is returned as the array element communalities[0], h22, as communalities[1] etc.
COMMUNALITY WEIGHTS
public double[] communalityWeights()Usage: weights = pca.communalityWeights()
This method returns all the communality weights, hi, where
bi,j are the loading factors (as rows) and n is the number of items. The communality weight, h1, is returned as the array element weight[0], h2, as weight[1] etc.
If a raw varimax rotation is used the communality weights used will all be set to unity.
VARIMAX ROTATION
VARIMAX SETTINGSpublic void setVarimaxTolerance(double tolerance)
public void setVarimaxMaximumIterations(int maximumIterations)
public int getVarimaxIterations()
Usage: pca.setVarimaxTolerance(tolerance)
This method sets the tolerance used to determine whether the maximization iteration in the varimax rotation has converged, i.e. whether two successve complete sets of pairwise rotations give values of the varimax criterion (see V below) that differ by less than the tolerance. The default value of the tolerance is 0.0001.
Usage: pca.setVarimaxMaximumIterations(maximumIterations)
This method sets the maximum number of iterations allowed by the maximization iteration in the varimax rotation. The default value is 1000. If this value is reached the current estimates of the rotated factors are returned.
Usage: iterations = pca.getVarimaxIterations()
This method returns the number of iterations used in the maximization iteration in the varimax rotation..
VARIMAX OPTIONS
public void useNormalVarimax()
public void useRawVarimax()
public String getVarimaxOption()
Usage: pca.useNormalVarimax()
This method sets the varimax option to that of the normal varimax criterion, i.e. the varimax criterion including weighting by the square roots of the relevant commmunalities; a rotation that maximizes
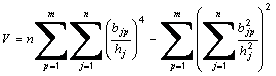
where bjp are the rotated loading factors for the m extracted factors and the n items and hj2 is the communality of the jth item taken over the m extracted factors.
Usage: pca.useRawVarimax()
This method sets the varimax option to that of the raw varimax criterion, i.e. the varimax criterion with NO weighting by the square roots of the relevant commmunalities; a rotation that maximizes
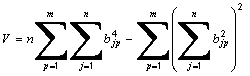
where bjp are the rotated loading factors for the m extracted factors and the n items.
Usage: option = pca.getNormalVarimax()
Returns the varimax option that is set as the default option, i.e. either "normal varimax option" or "raw varimax option".
PERFORM ROTATION
Instance methods
public void varimaxRotation(int nExtracted)
public void normalVarimaxRotation(int nExtracted)
public void rawVarimaxRotation(int nExtracted)
Usage: pca.varimaxRotation(nExtracted)
This method performs a varimax rotation on the nExtracted factors. The nExtracted factors are chosen as those with the nExtracted highest corrseponding unrotated eigenvalues. The varimax criterion option used is the default value, a normal varimax rotation if not reset, or the option reset by one of the methods described above.
Usage: pca.normalVarimaxRotation(nExtracted)
This method performs a varimax rotation on the nExtracted factors. The nExtracted factors are chosen as those with the nExtracted highest corrseponding unrotated eigenvalues. The varimax criterion option used is the normal varimax rotation irrespective of the instance's default option.
Usage: pca.rawVarimaxRotation(nExtracted)
This method performs a varimax rotation on the nExtracted factors. The nExtracted factors are chosen as those with the nExtracted highest corrseponding unrotated eigenvalues. The varimax criterion option used is the raw varimax rotation irrespective of the instance's default option.
Static methods
Static methods for performing a varimax rotation on a user supplied matrix are also provided.
public static double[][] normalVarimaxRotation(double[][] loadinFactors, double[] communalityWeights)
public static double[][] normalVarimaxRotation(double[][] loadinFactors, double[] communalityWeights, double tolerance, int[] maximumIterations)
public static double[][] rawVarimaxRotation(double[][] loadinFactors)
public static double[][] rawVarimaxRotation(double[][] loadinFactors, double tolerance, int[] maximumIterations)
public static double[][] transposeMatrix(double[][] matrix)
Usage: rotatedFactors = PCA.normalVarimaxRotation(loadingFactors, communalityWeights)
This method performs a normal varimax rotation on the matrix loadingFactors factors. The communality weights, communalityWeights should be the sum of the squares of the relevant loading factors. The rotated factors are returned as rotatedFactors. The loading factors must be entered as a loadings for a given factor as a row of the matrix. See transpose a matrix if your data has the factors arranged as columns. Default values of 0.0001 and 1000 are used for the tolerance and maximum number of iterations in the varimax iteration.
Usage: rotatedFactors = PCA.normalVarimaxRotation(loadingFactors, communalityWeights, tolerance, maximumIterations)
This method performs a normal varimax rotation on the matrix loadingFactors factors. The communality weights, communalityWeights should be the sum of the squares of the relevant loading factors. The rotated factors are returned as rotatedFactors. The loading factors must be entered as a loadings for a given factor as a row of the matrix. See transpose a matrix if your data has the factors arranged as columns. The tolerance and maximum number of iterations in the varimax iteration are supplied as the arguments tolerance and maximumIterations.
Usage: rotatedFactors = PCA.rawVarimaxRotation(loadingFactors)
This method performs a raw varimax rotation on the matrix loadingFactors factors. The rotated factors are returned as rotatedFactors. The loading factors must be entered as a loadings for a given factor as a row of the matrix. See transpose a matrix if your data has the factors arranged as columns. Default values of 0.0001 and 1000 are used for the tolerance and maximum number of iterations in the varimax iteration.
Usage: rotatedFactors = PCA.rawVarimaxRotation(loadingFactors, tolerance, maximumIterations)
This method performs a raw varimax rotation on the matrix loadingFactors factors. The rotated factors are returned as rotatedFactors. The loading factors must be entered as a loadings for a given factor as a row of the matrix. See transpose a matrix if your data has the factors arranged as columns. The tolerance and maximum number of iterations in the varimax iteration are supplied as the arguments tolerance and maximumIterations.
Usage: transpose = PCA.transposeMatrix(matrix)
This method returns the transpose of the matrix matrix. This methd is included for easy conversion of data stored as loading factors per item as matrix columns to a matrix with loading factors per item stored as rows. See Matrix class for full class of matrix manipulations.
ROTATED EIGENVALUES
public double[] rotatedEigenValues()
public double[] rotatedProportionPercentage()
public double[] rotatedCumulativePercentage()
Usage: eigenvalues = pca.rotatedEigenValues()
This method returns the rotated eigenvalues. These values are scaled so that the total variance associated with the extracted fators does not change on rotation.
Usage: proportions = pca.rotatedProportionPercentage()
This method returns the rotated eigenvalues expressed as a percentage of the total variance calculated using all unrotated eigenvalues. The returned values have been scaled so that the total variance associated with the extracted fators does not change on rotation.
Usage: cumulatives = pca.rotatedCumulativePercentage()
This method returns the rotated eigenvalues expressed as a cumulative percentage of the total variance calculated using all unrotated eigenvalues. The returned values have been scaled so that the total variance associated with the extracted fators does not change on rotation.
ROTATED LOADING FACTORS
public double[] rotatedLoadingFactorsAsRows()
public double[] rotatedLoadingFactorsAsColumns()
Usage: loadf = pca.rotatedLoadingFactorsAsRows()
This method returns the rotated loading factors corresponding to an eigenvalue returned as a row. These values are scaled so that the total variance associated with the extracted fators does not change on rotation.
Usage: loadf = pca.rotatedLoadingFactorsAsColumns()
This method returns the rotated loading factors corresponding to an eigenvalue returned as a column. These values are scaled so that the total variance associated with the extracted fators does not change on rotation.
KAISER-MEYER-OLKIN (KMO) STATISTIC [Measure of Sampling Adequacy (MSA)]
public double overallKMO()public double[] itemKMOs()
Usage: kmostatistic = pca.overallKMO()
This method returns the KMO [Kaiser-Meyer-Olkin] statistic:
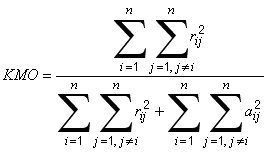
where rij are the elements of the correlation matrix, aij are the elements of the partial correlation matrix calculated as
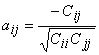
where Ckl are the cofactors of the correlation matrix and n is the number of items.
Usage: kmos = pca.itemKMOs()
This method returns the array of individual item KMO [Kaiser-Meyer-Olkin] statistics:
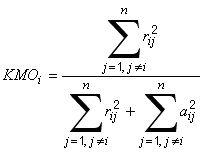
where rij are the elements of the correlation matrix, aij are the elements of the partial correlation matrix calculated as
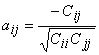
where Ckl are the cofactors of the correlation matrix and n is the number of items.
BARTLETT TEST OF SPHERICITY
public double chiSquareBartlett()Usage: chiSquare = pca.chiSquareBartlett()
This method returns the value of the Bartlett Test for Sphericity Chi-Square:
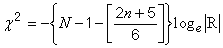
where N is the sample size. e.g. the number of persons, n is the number of items and |R| is the determinant of the correlation matrix.
public double probabilityBartlett()
Usage: significance = pca.probabilityBartlett()
This method returns the value of the Bartlett Test for Sphericity Chi-Square probability.
public int dofBartlett()
Usage: dof = pca.dofBartlett()
This method returns the value of the Bartlett Test for Sphericity Chi-Square degrees of freedom, n(n-1)/2, where n is the number of items.
X MATRIX
public Matrix xMatrix()Usage: xMatrix = pca.xMatrix()
This method returns the X matrix as an instance of Matrix. The X matrix is the data matrix with each element within a row (an itm) replaced by its value with the mean of the row subtracted and the result divided by the square root of the number of items minus one (or of the number of items - see set the denominator).
COVARIANCE MATRIX
public Matrix covarianceMatrix()Usage: covMatrix = pca.covarianceMatrix()
This method returns the covariance matrix as an instance of Matrix.
CORRELATION MATRIX
public Matrix correlationMatrix()Usage: corrMatrix = pca.correlationMatrix()
This method returns the correlation matrix as an instance of Matrix.
PARTIAL CORRELATION MATRIX
public Matrix partialCorrelationMatrix()Usage: partialCorrMatrix = pca.partialCorrelationMatrix()
This method returns the partial correlation matrix as an instance of Matrix.
TRANSPOSE OF THE X MATRIX
public Matrix xMatrixTranspose()Usage: xMatrixT = pca.xMatrixTranspose()
This method returns the transpose of the X matrix as an instance of Matrix. The X matrix is the data matrix with each element within a row (an itm) replaced by its value with the mean of the row subtracted and the result divided by the square root of the number of items minus one (or of the number of items - see set the denominator).
ORIGINAL DATA MATRIX
public Matrix originalMatrix()()Usage: data = pca.originalMatrix()()
This method returns the original data as an instance of Matrix.
DELETE AN ITEM
public double[][] deleteItem(String itemName)public double[][] deleteItem(int itemIndex)
Usage: newResponseMatrix = pca.deleteItem(itemName)
This method returns a matrix containing the entered data with the item with the name contained in the String itemName deleted. The returned matrix contains any 'no response' replacements in the remaining responses that were made in the original response matrix and will not contain any deletion made to the original data. The format of the returned matrix is responses of each item per column.
Usage: newResponseMatrix = pca.deleteItem(itemIndex)
This method returns a matrix containing the entered data with the item of index itemIndex deleted. The indices run from 1 to n. The returned matrix contains any 'no response' replacements in the remaining responses that were made in the original response matrix and will not contain any deletion made to the original data. The format of the returned matrix is responses of each item per column.
SCATTER PLOTS
Plot of item - item responsespublic void rawItemItemPlot(String itemName1, String itemName2)
public void rawItemItemPlot(int item1Index1, int itemIndex2)
public void standardizedItemItemPlot(String itemName1, String itemName2)
public void standardizedItemItemPlot(int item1Index1, int itemIndex2)
Usage: pca.rawItemItemPlot(itemName1, itemName2)
Calling this method displays, in a new window, a plot of the raw data responses of the item named itemName1 against the raw data responses of the item named itemName2.
Usage: pca.rawItemItemPlot(itemIndex1, itemIndex2)
Calling this method displays, in a new window, a plot of the raw data responses of the item with an index itemIndex1 against the raw data responses of the item with an index itemIndex2. NOTE!! the item indices start at 1 not at 0. See Item Names for methods that return an item index or name.
Usage: pca.standardizedItemItemPlot(itemName1, itemName2)
Calling this method displays, in a new window, a plot of the standardized data responses of the item named itemName1 against the standardized data responses of the item named itemName2.
Usage: pca.standardizedItemItemPlot(itemIndex1, itemIndex2)
Calling this method displays, in a new window, a plot of the standardized data responses of the item with an index itemIndex1 against the standardized data responses of the item with an index itemIndex2. NOTE!! the item indices start at 1 not at 0. See Item Names for methods that return an item index or name.
Plot of item - means of item responses
public void rawItemMeansPlot(String itemName)
public void rawItemMeansPlot(int item1Index)
public void standardizedItemMeansPlot(String itemName)
public void standardizedItemMeansPlot(int item1Index)
Usage: pca.rawItemMeansPlot(itemName)
Calling this method displays, in a new window, a plot of the raw data responses of the item named itemName against the means of the raw data responses of all items.
Usage: pca.rawItemMeansPlot(itemIndex)
Calling this method displays, in a new window, a plot of the raw data responses of the item with an index itemIndex a against the means of the raw data responses of all items. NOTE!! the item indices start at 1 not at 0. See Item Names for methods that return an item index or name.
Usage: pca.standardizedItemMeansPlot(itemName)
Calling this method displays, in a new window, a plot of the standardized data responses of the item named itemName against the means of the standardized data responses of all items.
Usage: pca.standardizedItemMeansPlot(itemIndex)
Calling this method displays, in a new window, a plot of the standardized data responses of the item with an index itemIndex against the means of the standardized data responses of all items. NOTE!! the item indices start at 1 not at 0. See Item Names for methods that return an item index or name.
CORRELATION COEFFICIENTS
BETWEEN ALL ITEMSCorrelation Coefficient Matrix
public double[][] rawCorrelationCoefficients()
public double[][] standardizedCorrelationCoefficients()
Usage: corrCoeff = pca.rawCorrelationCoefficients()
This method returns an (n+1) times (n+1) matrix where n is the number of items. Rows and columns 0 to n-1 contain the correlation coefficients, for the raw data responses, between all pairs of items, e.g. corrCoeff[0][3] contains the correlation coefficient between the first item and the fourth item. Rows and columns n contain the correlation coefficients between the items and the totals of all the items, e.g. corrCoeff[1][n] contains the correlation coefficient, for the raw data responses, between the second item and the totals of all n items.
Usage: corrCoeff = pca.standardizedCorrelationCoefficients()
This method returns an (n+1) times (n+1) matrix where n is the number of items. Rows and columns 0 to n-1 contain the correlation coefficients, for the standardized data responses, between all pairs of items, e.g. corrCoeff[0][3] contains the correlation coefficient between the first item and the fourth item. Rows and columns n contain the correlation coefficients between the items and the totals of all the items, e.g. corrCoeff[1][n] contains the correlation coefficient, for the standardized data responses, between the second item and the totals of all n items.
Average correlation coefficient, excluding totals
public double rawAverageCorrelationCoefficients()
public double standardizedAverageCorrelationCoefficients()
Usage: meanCorrCoeff = pca.rawAverageCorrelationCoefficients()
This method returns, for the raw data responses, the average of all the correlation coefficients between items,
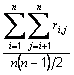
where n is the number of items and ri,j is the correlation coefficient between the ith and jth items. This method does not include, in the average, the correlation coefficients with the totals of all the items (see below).
Usage: meanCorrCoeff = pca.standardizedAverageCorrelationCoefficients()
This method returns, for the standardized data responses, the average of all the correlation coefficients between items,
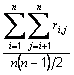
where n is the number of items and ri,j is the correlation coefficient between the ith and jth items. This method does not include, in the average, the correlation coefficients with the totals of all the items (see below).
Average correlation coefficient, including totals
public double rawStandardDeviationCorrelationCoefficientsWithTotals()
public double standardizedStandardDeviationCorrelationCoefficientsWithTotals()
Usage: meanCorrCoeff = pca.rawStandardDeviationCorrelationCoefficientsWithTotals()
This method returns, for the raw data responses, the average of all the correlation coefficients between items and the totals of all items,
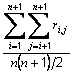
where n is the number of items and ri,j, for i and j less than or equal to n is the correlation coefficient between the ith and jth items and ri,n+1 is the correlation coefficient between the ith item and the totals of all items. See above) for exclusion of totals.
Usage: meanCorrCoeff = pca.standardizedStandardDeviationCorrelationCoefficientsWithTotals()
This method returns, for the standardized data responses, the average of all the correlation coefficients between items and the totals of all items,
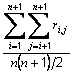
where n is the number of items and ri,j, for i and j less than or equal to n is the correlation coefficient between the ith and jth items and ri,n+1 is the correlation coefficient between the ith item and the totals of all items. See above for exclusion of totals.
Standard deviation of the correlation coefficients, excluding totals
public double rawStandardDeviationCorrelationCoefficients()
public double standardizedStandardDeviationCorrelationCoefficients()
Usage: sdCorrCoeff = pca.rawStandardDeviationCorrelationCoefficients()
This method returns, for the raw data responses, the standard deviation of all the correlation coefficients between items. This method does not include, in the average, the correlation coefficients with the totals of all the items (see below).
Usage: sdCorrCoeff = pca.standardizedStandardDeviationCorrelationCoefficients()
This method returns, for the standardized data responses, the standard deviation of all the correlation coefficients between items. This method does not include, in the average, the correlation coefficients with the totals of all the items (see below).
Standard deviation of the correlation coefficients, including totals
public double rawStandardDeviationCorrelationCoefficientsWithTotals()
public double standardizedStandardDeviationCorrelationCoefficientsWithTotals()
Usage: sdCorrCoeff = pca.rawStandardDeviationCorrelationCoefficientsWithTotals()
This method returns, for the raw data responses, the standard deviation of all the correlation coefficients between items and the totals of all items. See above) for exclusion of totals.
Usage: sdCorrCoeff = pca.standardizedStandardDeviationCorrelationCoefficientsWithTotals()
This method returns, for the standardized data responses, the standard deviation of all the correlation coefficients between items and the totals of all items. See above for exclusion of totals.
BETWEEN PAIRS
Item-item pair
public double rawCorrelationCoefficient(String itemName1, String itemName2)
public double rawCorrelationCoefficient(int itemIndex1, int itemIndex2)
public double standardizedCorrelationCoefficient(String itemName1, String itemName2)
public double standardizedCorrelationCoefficient(int itemIndex1, int itemIndex2)
Usage: corrCoeff = pca.rawCorrelationCoefficient(itemName1, itemName2)
This method returns the correlation coefficient, for the raw data responses, between the item with the name contained in the String itemName1 and the item with the name contained in the String itemName2.
Usage: corrCoeff = pca.rawCorrelationCoefficient(itemIndex1, itemIndex2)
This method returns the correlation coefficient, for the raw data responses, between the item of index itemIndex1 and the item of index itemIndex2. The indices run from 1 to n.
Usage: corrCoeff = pca.standardizedCorrelationCoefficient(itemName1, itemName2)
This method returns the correlation coefficient, for the standardized data responses, between the item with the name contained in the String itemName1 and the item with the name contained in the String itemName2.
Usage: corrCoeff = pca.standardizedCorrelationCoefficient(itemIndex1, itemIndex2)
This method returns the correlation coefficient, for the standardized data responses, between the item of index itemIndex1 and the item of index itemIndex2. The indices run from 1 to n.
Item-(totals of all items) pair
public double rawCorrelationCoefficient(String itemName)
public double rawCorrelationCoefficient(int itemIndex)
public double standardizedCorrelationCoefficient(String itemName)
public double standardizedCorrelationCoefficient(int itemIndex)
Usage: corrCoeff = pca.rawCorrelationCoefficient(itemName)
This method returns the correlation coefficient, for the raw data responses, between the item with the name contained in the String itemName and the totals of all items.
Usage: corrCoeff = pca.rawCorrelationCoefficient(itemIndex)
This method returns the correlation coefficient, for the raw data responses, between the item of index itemIndex and the totals of all items. The indices run from 1 to n.
Usage: corrCoeff = pca.standardizedCorrelationCoefficient(itemName1)
This method returns the correlation coefficient, for the standardized data responses, between the item with the name contained in the String itemName1 and the totals of all items.
Usage: corrCoeff = pca.standardizedCorrelationCoefficient(itemIndex)
This method returns the correlation coefficient, for the standardized data responses, between the item of index itemIndex aand the totals of all items. The indices run from 1 to n.
COVARIANCES
BETWEEN ALL ITEMSCovariance Matrix
public double[][] rawCovariances()
public double[][] standardizedCovariances()
Usage: covar = pca.rawCovariances()
This method returns an (n+1) times (n+1) matrix where n is the number of items. Rows and columns 0 to n-1 contain the covariances, for the raw data responses, between all pairs of items, e.g. corrCoeff[0][3] contains the covariance between the first item and the fourth item. Rows and columns n contain the covariances between the items and the totals of all the items, e.g. corrCoeff[1][n] contains the covariance, for the raw data responses, between the second item and the totals of all n items. The diagonal elements contain the variances, e.g. covar[2][2] contins the variance of the third item.
See Setting the denominator for covariance formulae options.
Usage: covar = pca.standardizedCovariances()
This method returns an (n+1) times (n+1) matrix where n is the number of items. Rows and columns 0 to n-1 contain the covariances, for the standardized data responses, between all pairs of items, e.g. corrCoeff[0][3] contains the covariance between the first item and the fourth item. Rows and columns n contain the covariances between the items and the totals of all the items, e.g. corrCoeff[1][n] contains the covariance, for the standardized data responses, between the second item and the totals of all n items. The diagonal elements contain the variances, e.g. covar[2][2] contins the variance of the third item.
See Setting the denominator for covariance formulae options.
BETWEEN PAIRS
Item-item pair
public double rawCovariance(String itemName1, String itemName2)
public double rawCovariance(int itemIndex1, int itemIndex2)
public double standardizedCovariance(String itemName1, String itemName2)
public double standardizedCovariance(int itemIndex1, int itemIndex2)
Usage: covar = pca.rawCovariance(itemName1, itemName2)
This method returns the covariance, for the raw data responses, between the item with the name contained in the String itemName1 and the item with the name contained in the String itemName2.
Usage: covar = pca.rawCovariance(itemIndex1, itemIndex2)
This method returns the covariance, for the raw data responses, between the item of index itemIndex1 and the item of index itemIndex2. The indices run from 1 to n.
Usage: covar = pca.standardizedCovariance(itemName1, itemName2)
This method returns the covariance, for the standardized data responses, between the item with the name contained in the String itemName1 and the item with the name contained in the String itemName2.
Usage: covar = pca.standardizedCovariance(itemIndex1, itemIndex2)
This method returns the covariance, for the standardized data responses, between the item of index itemIndex1 and the item of index itemIndex2. The indices run from 1 to n.
See Setting the denominator for covariance formulae options.
Item-(totals of all items) pair
public double rawCovariance(String itemName)
public double rawCovariance(int itemIndex)
public double standardizedCovariance(String itemName)
public double standardizedCovariance(int itemIndex)
Usage: covar = pca.rawCovariance(itemName)
This method returns the covariance, for the raw data responses, between the item with the name contained in the String itemName and the totals of all items.
Usage: covar = pca.rawCovariance(itemIndex)
This method returns the covariance, for the raw data responses, between the item of index itemIndex and the totals of all items. The indices run from 1 to n.
Usage: covar = pca.standardizedCovariance(itemName1)
This method returns the covariance, for the standardized data responses, between the item with the name contained in the String itemName1 and the totals of all items.
Usage: covar = pca.standardizedCovariance(itemIndex)
This method returns the covariance, for the standardized data responses, between the item of index itemIndex aand the totals of all items. The indices run from 1 to n.
See Setting the denominator for covariance formulae options.
ITEM MEANS
MEAN VALUES OF ALL ITEMSRaw data
public double[] rawItemMeans()
Usage: itemMeans = pca.rawItemMeans()
This method returns the means, calculated using the raw data, of all the items. The order of items is as entered minus any deleted due to missing responses.
Standardized data
public double[] standardizedItemMeans()
Usage: itemMeans = pca.standardizedItemMeans()
This method returns the means, calculated using standardized data, of all the items. The order of items is as entered minus any deleted due to missing responses.
MEAN VALUE OF AN INDIVIDUAL ITEM
Raw data
public double rawItemMean(int index)
public double rawItemMean(String name)
Usage: itemMean = pca.rawItemMean(item)
This method returns the mean, calculated using the raw data, of an individual item. The item may be identified (argument item) by its index or its name. Note that the order of items starts at 1 and NOT 0. The order is as entered minus any deleted due to missing responses.
Standardized data
public double standardizedItemMean(int index)
public double standardizedItemMean(String name)
Usage: itemMean = pca.standardizedItemMean(item)
This method returns the mean, calculated using standardized data, of an individual item. The item may be identified (argument item) by its index or its name. Note that the order of items starts at 1 and NOT 0. The order is as entered minus any deleted due to missing responses.
MEAN VALUE OF ALL ITEM MEANS
Raw data
public double rawMeanOfItemMeans()
Usage: itemMeanOfMeans = pca.rawMeanOfItemMeans()
This method returns the mean, calculated using the raw data, of the means of all items.
Standardized data
public double standardizedMeanOfItemMeans()
Usage: itemMeanOfMeans = pca.standardizedMeanOfItemMeans()
This method returns the mean, calculated using standardized data, of the means of all items.
STANDARD DEVIATION OF ALL ITEM MEANS
Raw data
public double rawStandardDeviationOfItemMeans()
Usage: itemSdOfMeans = pca.rawStandardDeviationOfItemMeans()
This method returns the standard deviation, calculated using the raw data, of the means of all items.
Standardized data
public double[] standardizedStandardDeviationOfItemMeans()
Usage: itemSdOfMeans = pca.standardizedStandardDeviationOfItemMeans()
This method returns the standard deviation, calculated using standardized data, of the means of all items.
See Setting the denominator for standard deviation formulae options.
VARIANCE OF ALL ITEM MEANS
Raw data
public double rawVarianceOfItemMeans()
Usage: itemVarOfMeans = pca.rawVarianceOfItemMeans()
This method returns the variance, calculated using the raw data, of the means of all items.
Standardized data
public double[] standardizedVarianceOfItemMeans()
Usage: itemVarOfMeans = pca.standardizedVarianceOfItemMeans()
This method returns the variance, calculated using standardized data, of the means of all items.
See Setting the denominator for variance formulae options.
MAXIMUM OF ALL ITEM MEANS
Raw data
public double rawMaximumOfItemMeans()
Usage: itemMaxOfMeans = pca.rawMaximumOfItemMeans()
This method returns the maximum, calculated using the raw data, of the means of all items.
Standardized data
public double[] standardizedMaximumOfItemMeans()
Usage: itemMaxOfMeans = pca.standardizedMaximumOfItemMeans()
This method returns the maximum, calculated using standardized data, of the means of all items.
MINIMUM OF ALL ITEM MEANS
Raw data
public double rawMinimumOfItemMeans()
Usage: itemMinOfMeans = pca.rawMinimumOfItemMeans()
This method returns the minimum, calculated using the raw data, of the means of all items.
Standardized data
public double[] standardizedMinimumOfItemMeans()
Usage: itemMinOfMeans = pca.standardizedMinimumOfItemMeans()
This method returns the minimum, calculated using standardized data, of the means of all items.
RANGE OF ALL ITEM MEANS
Raw data
public double rawRangeOfItemMeans()
Usage: itemRangeOfMeans = pca.rawRangeOfItemMeans()
This method returns the range, calculated using the raw data, of the means of all items.
Standardized data
public double[] standardizedRangeOfItemMeans()
Usage: itemRangeOfMeans = pca.standardizedRangeOfItemMeans()
This method returns the range, calculated using standardized data, of the means of all items.
ITEM MOMENT SKEWNESS
The moment skewness of an item is defined as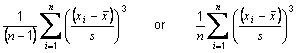
where xi are the responses to the item in question,
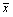is the sample mean of the item and s is the sample standard deviation of the item.The default denominator is (n−1). See Setting the denominator for methods resetting the denominator.
MOMENT SKEWNESS OF ALL ITEMS
Raw data
public double[] rawItemMomentSkewnessess()
Usage: skewness = pca.rawItemMomentSkewnessess()
This method returns the moment skewnesses, calculated using the raw data, of all the items. The order of items is as entered minus any deleted due to missing responses.
Standardized data
public double[] standardizedItemMomentSkewnessess() Usage: skewness = pca.standardizedItemMomentSkewnessess()
This method returns the moment skewnesses, calculated using standardized data, of all the items. The order of items is as entered minus any deleted due to missing responses.
MOMENT SKEWNESS OF AN INDIVIDUAL ITEM
Raw data
public double rawItemMomentSkewness(int index)
public double rawItemMomentSkewness(String name)
Usage: skewness = pca.rawItemMomentSkewness(item)
This method returns the moment skewness, calculated using the raw data, of an individual item. The item may be identified (argument item) by its index or its name. Note that the order of items starts at 1 and NOT 0. The order is as entered minus any deleted due to missing responses.
Standardized data
public double standardizedItemMomentSkewness(int index)
public double standardizedItemMomentSkewness(String name)
Usage: skewness = pca.standardizedItemMomentSkewness(item)
This method returns the moment skewness, calculated using standardized data, of an individual item. The item may be identified (argument item) by its index or its name. Note that the order of items starts at 1 and NOT 0. The order is as entered minus any deleted due to missing responses.
ITEM MEDIAN SKEWNESS (Pearson's median skewness coefficient)
The median skewness of an item is defined as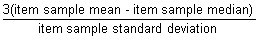
See Setting the denominator for standard deviation formulae options.
MEDIAN SKEWNESS OF ALL ITEMS
Raw data
public double[] rawItemMedianSkewnessess()
Usage: skewness = pca.rawItemMedianSkewnessess()
This method returns the median skewnesses, calculated using the raw data, of all the items. The order of items is as entered minus any deleted due to missing responses.
Standardized data
public double[] standardizedItemMedianSkewnessess()
Usage: skewness = pca.standardizedItemMedianSkewnessess()
This method returns the median skewnesses, calculated using standardized data, of all the items. The order of items is as entered minus any deleted due to missing responses.
MEDIAN SKEWNESS OF AN INDIVIDUAL ITEM
Raw data
public double rawItemMedianSkewness(int index)
public double rawItemMedianSkewness(String name)
Usage: skewness = pca.rawItemMedianSkewness(item)
This method returns the median skewness, calculated using the raw data, of an individual item. The item may be identified (argument item) by its index or its name. Note that the order of items starts at 1 and NOT 0. The order is as entered minus any deleted due to missing responses.
Standardized data
public double standardizedItemMedianSkewness(int index)
public double standardizedItemMedianSkewness(String name)
Usage: skewness = pca.standardizedItemMedianSkewness(item)
This method returns the median skewness, calculated using standardized data, of an individual item. The item may be identified (argument item) by its index or its name. Note that the order of items starts at 1 and NOT 0. The order is as entered minus any deleted due to missing responses.
ITEM QUARTILE SKEWNESS (Bowley skewness coefficient)
The quartile skewness of an item is defined as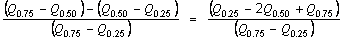
where the Qs denote the interquartile ranges of the item.
QUARTILE SKEWNESS OF ALL ITEMS
Raw data
public double[] rawItemMedianSkewnessess()
Usage: skewness = pca.rawItemQuartileSkewnessess()
This method returns the quartile skewnesses, calculated using the raw data, of all the items. The order of items is as entered minus any deleted due to missing responses.
Standardized data
public double[] rawItemQuartileSkewnessess()
Usage: skewness = pca.standardizedItemQuartileSkewnessess()
This method returns the quartile skewnesses, calculated using standardized data, of all the items. The order of items is as entered minus any deleted due to missing responses.
QUARTILE SKEWNESS OF AN INDIVIDUAL ITEM
Raw data
public double rawItemQuartileSkewness(int index)
public double rawItemQuartileSkewness(String name)
Usage: skewness = pca.rawItemMedianSkewness(item)
This method returns the quartile skewness, calculated using the raw data, of an individual item. The item may be identified (argument item) by its index or its name. Note that the order of items starts at 1 and NOT 0. The order is as entered minus any deleted due to missing responses.
Standardized data
public double standardizedItemQuartileSkewness(int index)
public double standardizedItemQuartileSkewness(String name)
Usage: skewness = pca.standardizedItemMedianSkewness(item)
This method returns the quartile skewness, calculated using standardized data, of an individual item. The item may be identified (argument item) by its index or its name. Note that the order of items starts at 1 and NOT 0. The order is as entered minus any deleted due to missing responses.
ITEM EXCESS KURTOSIS
The excess kurtosis of an item is defined as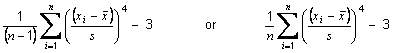
where xi are the responses to the item in question,
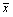is the sample mean of the item and s is the sample standard deviation opf the item, i.e. returns the kurtosis of the item minus the kurtosis of a Gaussian distribution (3.0).The default denominator is (n−1). See Setting the denominator for methods resetting the denominator.
EXCESS KURTOSES OF ALL ITEMS
Raw data
public double[] rawItemExcessKurtoses()
Usage: kurtoses = pca.rawItemExcessKurtoses()
This method returns the excess kurtoses, calculated using the raw data, of all the items. The order of items is as entered minus any deleted due to missing responses.
Standardized data
public double[] standardizedItemExcesskurtoses()
Usage: kurtoses = pca.standardizedItemExcesskurtoses()
This method returns the excess kurtoses, calculated using standardized data, of all the items. The order of items is as entered minus any deleted due to missing responses.
EXCESS KURTOSIS OF AN INDIVIDUAL ITEM
Raw data
public double rawItemExcessKurtosis(int index)
public double rawItemExcessKurtosis(String name)
Usage: kurtosis = pca.rawItemExcessKurtosis(item)
This method returns the excess kurtosis, calculated using the raw data, of an individual item. The item may be identified (argument item) by its index or its name. Note that the order of items starts at 1 and NOT 0. The order is as entered minus any deleted due to missing responses.
Standardized data
public double standardizedItemExcessKurtosis(int index)
public double standardizedItemExcessKurtosis(String name)
Usage: kurtosis = pca.standardizedItemExcessKurtosis(item)
This method returns the excess kurtosis, calculated using standardized data, of an individual item. The item may be identified (argument item) by its index or its name. Note that the order of items starts at 1 and NOT 0. The order is as entered minus any deleted due to missing responses.
ITEM NAMES AND INDICES
NAMES OF THE USED ITEMSpublic String[] itemNames()
Usage: names = pca.itemNames()
This method returns the names of the items used, i.e. after any deletions due to 'missing responses'.
NAMES OF THE ENTERED ITEMS
public String[] originalItemNames()
Usage: names = pca.originalItemNames()
This method returns the names of the items originally entered, i.e. before any deletions due to 'missing responses'.
NAMES OF ANY DELETED ITEMS
public String[] deletedItemsNames()
Usage: names = pca.deletedItemsNames()
This method returns the names of items originally entered but then deleted as part of the 'missing responses' handling. If no items have been deleted null is returned.
INDEX OF AN ITEM
public int itemIndex(String name)
Usage: index = pca.itemIndex(name)
This method returns the index of the item whose name is passed to the method as the argument name. NOTE the indices of names start at 1 and NOT at zero.
NAME OF AN ITEM
public String itemName(int index)
Usage: name = pca.itemName(index)
This method returns the name of the item whose index is passed to the method as the argument index. NOTE the indices of names start at 1 and NOT at zero.
NUMBER OF ITEMS
Number of items usedpublic int usedNumbeOfItems()
Usage: num = pca.usedNumbeOfItems()
This method returns the number of items used, i.e. after any deletions due to the 'missing response' handling.
Number of items entered
public int originalNumbeOfItems()
Usage: num = pca.originalNumbeOfItems()
This method returns the number of items entered, i.e. before any deletions due to the 'missing response' handling.
Number of items deleted
public int numbeOfDeletedItems()
Usage: num = pca.numbeOfDeletedItems()
This method returns the number of items deleted due to the 'missing response' handling.
PERSON INDICES
INDICES OF THE USED PERSONSpublic String[] personIndices()
Usage: names = pca.personIndices()
This method returns the indices of the persons used, i.e. after any deletions due to 'missing responses'. NOTE the indices of the persons start at 1 and NOT at zero.
INDICES OF ANY DELETED PERSONSS
public String[] deletedPersonsIndices()
Usage: names = pca.deletedPersonsIndices()
This method returns the indices of items originally entered but then deleted as part of the 'missing responses' handling. NOTE the indices of the persons start at 1 and NOT at zero.
NUMBER OF PERSONS
Number of persons usedpublic int usedNumbeOfPersons()
Usage: num = pca.usedNumbeOfPersons()
This method returns the number of persons used, i.e. after any deletions due to the 'missing response' handling.
Number of persons entered
public int originalNumbeOfPersons()
Usage: num = pca.originalNumbeOfPersons()
This method returns the number of persons entered, i.e. before any deletions due to the 'missing response' handling.
Number of persons deleted
public int numbeOfDeletedPersons()
Usage: num = pca.numbeOfDeletedPersons()
This method returns the number of persons deleted due to the 'missing response' handling.
RESPONSES
ORIGINAL RESONSESResponses as originally entered
public Object originalScores()
Usage: originalData = pca.originalScores()
This method returns the responses as originally entered, i.e. before any deletions. They are returned as a Java Object as they may have been entered as String[][], double[][], float[][], int[][], char[][], boolean[][] or Matrix. If they were originally read in from a text file the returned Object is of type String[][].
Original responses as row per item
public double[][] originalScoresAsRowPerItem()
Usage: originalData = pca.originalScoresAsRowPerItem()
This method returns the original responses entered rearranged as a two dimensional array of doubles orgainized as a row of responses for each item. Missing responses are returned as Double.NaN.
Original responses as row per person
public double[][] originalScoresAsRowPerPerson()
Usage: originalData = pca.originalScoresAsRowPerPerson()
This method returns the original responses entered rearranged as a two dimensional array of doubles orgainized as a row of responses for each person. Missing responses are returned as Double.NaN.
RESPONSES AS USED (RAW DATA)
Responses as used as row per item
public double[][] usedScoresAsRowPerItem()
Usage: data = pca.usedScoresAsRowPerItem()
This method returns the raw data responses as used, i.e. minus any deleted items or persons, arranged as a two dimensional array of doubles orgainized as a row of responses for each item. Retained missing responses are returned with the chosen substituted values.
Responses as used as row per person
public double[][] usedScoresAsRowPerItem()
Usage: data = pca.usedScoresAsRowPerPerson()
This method returns the raw data responses as used, i.e. minus any deleted items or persons, arranged as a two dimensional array of doubles orgainized as a row of responses for each person. Retained missing responses are returned with the chosen substituted values.
RESPONSES AS USED (STANDARDIZED DATA)
Standardized responses as used as row per item
public double[][] standardizedScoresAsRowPerItem()
Usage: data = pca.standardizedScoresAsRowPerItem()
This method returns the standardized data responses as used, i.e. minus any deleted items or persons, arranged as a two dimensional array of doubles orgainized as a row of responses for each item. Retained missing responses are returned with the chosen standardized substituted values.
Standardized responses as used as row per person
public double[][] standardizedScoresAsRowPerItem()
Usage: data = pca.standardizedScoresAsRowPerPerson()
This method returns the standardized data responses as used, i.e. minus any deleted items or persons, arranged as a two dimensional array of doubles orgainized as a row of responses for each person. Retained missing responses are returned with the chosen standardized substituted values.
ITEM NAME AND PERSON INDEX OF THE REPLACED RESPONSES
Standardized responses as used as row per item
public String[] indicesOfReplacedScores()
Usage: repl = pca.ndicesOfReplacedScores()
This method returns the item name and person index for all 'missing responses' that have been replaced rather than deleted. NOTE that the indices of the persons starts at 1 NOT at 0.
NUMBER OF RESPONSES
Original number of scores
public int originalTotalNumberOfScores()
Usage: nScores = pca.originalTotalNumberOfScores()
This method returns the original number of responses entered, i.e. before any deletions.
Number of scores used
public int usedTotalNumberOfScores()
Usage: nScores = pca.usedTotalNumberOfScores()
This method returns the number of responses used, i.e. after any deletions.
Number of deleted scores
public int numberOfDeletedScores()
Usage: nDeletes = pca.numberOfDeletedScores()
This method returns the number of responses that have been deleted in the handling of any 'missing responses'.
Number of replacement scores
public int numberOfReplacedScores()
Usage: nDeletes = pca.numberOfReplacedScores()
This method returns the number of responses that have been replaced in the handling of any 'missing responses'.
SOME OF THE DOCUMENTATION IS STILL UNDER CONSTRUCTION
Some of the item statistic methods, e.g. rawItemStandardDeviation(), person statistic methods, e.g. standardizedPersonVariances(), and allResponses statistic methods, e.g. rawAllResponsesMaximum(), have still to be fully documented. All of these follow the same format as that of the corresponding methods in the Item Means methods documented above. Their full individual documentation will be added later.
EXAMPLE PROGRAM
An example program, PCA_Analysis, and the associated documentation may be found on PCA Analysis.BIBLIOGRAPHY
Cohen, L., Manion, L. & Morrison, K, A. (2008), Research Methods in Education, 6th Edition, Routledge, London & New York, Chapter twenty five, Multidimensional measurement and factor analysis, pp 559-585.Harman, H. H. (1976), Modern Factor Analysis, 3rd Edition Revised, The University of Chigago Press, Chicago & London.
OTHER CLASSES USED BY THIS CLASS
This class uses the following classes in this library:This page was prepared by Dr Michael Thomas Flanagan