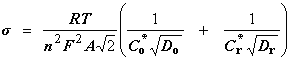| |
Michael Thomas Flanagan's Java Scientific Library
ImpedSpecRegression Class: Impedance Spectroscopy Regression
|
|
|
Last update: 5 July 2008
This class provides the methods for fitting complex impedance versus frequency data, as typically obtained in impedance spectroscopy (IS) and in electrochemical impedance spectroscopy (EIS), to a circuit model. Such data is typically obtained using voltage divider in which one impedance is the circuit to be examined, or a system that can be represented by an equivalent circuit (test or model circuit), and the other impedance is the reference impedance, often simply a resistor of known value:
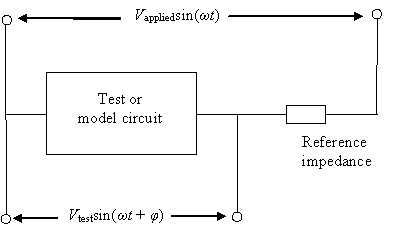
The data may be entered as:
- the magnitudes, Vtest, and phases, φ of the voltage across the test or model circuit as a function of frequency, ω
- the real and imaginary parts of the voltage across the test or model circuit as a function of frequency, ω
- the magnitudes and phases of the impedance of the test or model circuit as a function of frequency, ω
- the real and imaginary parts of the impedance of the test or model circuit as a function of frequency, ω.
Options 1 and 2 require that the applied voltage, Vapplied, and the reference impedance also be entered.
Options 3 and 4 allow for the analysis of data obtained using analytical arrangements other than the above.
The test or model circuit may be provided by the user, and is implemented via an interface, ImpedSpecModel, or may be chosen from one of the range of 44 model circuits provided by this class.
The circuit may contain any or all of the following electrical or electrochemical components:
- Resistor [complex impedance: R + j0]
- Capacitor [complex impedance: 0 − j/Cω]
- Inductor [complex impedance: 0 + jLω]
- Constant Phase Element [complex impedance: σ(jω)−α]
- Warburg Impedance (infinite diffusion layer thickness) [complex impedance: σ/ω0.5 − jσ/ω0.5]
- Warburg Impedance (finite diffusion layer thickness) [complex impedance: σ/ω0.5(1 − j)tanh[δ(jω)0.5]]
The symbol, j, is used on this page to represent the square root of minus one.
This class, ImpedSpecRegression, is a subclass of the superclass Regression and all the methods in the Regression class may be called in addition to those methods listed on this page.
A Nelder and Mead simplex based non-linear regression is used with the frequencies as the independent variable and the real parts and the imaginary parts of the test circuit complex impedance as the dependent variables. See the Regression class for details of the Nelder and Mead non-linear regression procedure. The regression procedure is called twice; firstly with the user supplied or class calculated initial estimates, secondly with the best estimates from the first regression call as the initial estimates.
|
import statement:
|
import flanagan.circuits.ImpedSpecRegression;
import flanagan.circuits.ImpedSpecRegressionFunction1; (only for precompiled model circuits)
import flanagan.circuits.ImpedSpecRegressionFunction2; (only for user supplied circuits)
import flanagan.circuits.ImpedSpecModel; (only for user supplied circuits)
|
Related classes
SUMMARY OF CONSTRUCTORS AND METHODS
|
Constructors |
|
public ImpedSpecRegression()
|
|
public ImpedSpecRegression(String title)
|
|
Enter the circuit model
|
Choose a listed circuit model
|
public void setModel(int modelNumber)
|
public void setModel(int modelNumber, double[ ] initialEstimates)
|
|
public void setModel(int modelNumber, double[ ] initialEstimates, double[ ] initialSteps)
|
|
Enter a user coded circuit model
|
public void setModel(ImpedSpecModel userModel, String[ ] symbols, double[ ] initialEstimates)
|
|
public void setModel(ImpedSpecModel userModel, String[ ] symbols, double[ ] initialEstimates, double[ ] initialSteps)
|
|
Get circuit model details
|
public double[] getInitialEstimates()
|
|
public String[] getCircuitComponents()
|
|
Enter the experimental data
|
Enter the reference impedance
|
public void setReferenceImpedance(double resistance)
|
public void setReferenceImpedance(double referenceRealZ, double referenceImagZ)
|
public void setReferenceImpedance(Complex referenceImpedance)
|
|
Enter the applied voltage
|
public void setAppliedVoltage(double appliedVoltage)
|
|
public void setAppliedVoltage(double appliedVoltage, double appliedVoltageError)
|
|
Enter the experimental data as voltage
|
public void voltageDataAsPhasorRad(double[] frequencies, double[] voltageMagnitudes, double[] voltagePhasesRad)
|
|
public void voltageDataAsPhasorRad(double[] frequencies, double[] voltageMagnitudes,double[] voltagePhasesRad, double[] voltageMagWeights, double[] voltagePhaseWeights)
|
|
public void voltageDataAsPhasorDeg(double[] frequencies, double[] voltageMagnitudes,double[] voltagePhasesDeg)
|
|
public void voltageDataAsPhasorDeg(double[] frequencies, double[] voltageMagnitudes,double[] voltagePhasesDeg, double[] voltageMagWeights, double[] voltagePhaseWeights)
|
|
public void voltageDataAsComplex(double[] frequencies, double[] real,double[] imag)
|
|
public void voltageDataAsComplex(double[] frequencies, double[] real,double[] imag, double[] realWeights, double[] imagWeights)
|
|
public void voltageDataAsComplex(double[] frequencies, Complex[] voltages)
|
|
public void voltageDataAsComplex(double[] frequencies, Complex[] voltages, Complex[] voltageWeights)
|
|
Enter the experimental data as impedance
|
public void impedanceDataAsPhasorRad(double[] frequencies, double[] impedanceMagnitudes, double[] impedancePhasesRad)
|
|
public void impedanceDataAsPhasorRad(double[] frequencies, double[] impedanceMagnitudes,double[] impedancePhasesRad, double[] impedanceMagWeights, double[] impedancePhaseWeights)
|
|
public void impedanceDataAsPhasorDeg(double[] frequencies, double[] impedanceMagnitudes,double[] impedancePhasesDeg)
|
|
public void impedanceDataAsPhasorDeg(double[] frequencies, double[] impedanceMagnitudes,double[] impedancePhasesDeg, double[] impedanceMagWeights, double[] impedancePhaseWeights)
|
|
public void impedanceDataAsComplex(double[] frequencies, double[] real,double[] imag)
|
|
public void impedanceDataAsComplex(double[] frequencies, double[] real,double[] imag, double[] realWeights, double[] imagWeights)
|
|
public void impedanceDataAsComplex(double[] frequencies, Complex[] impedances)
|
|
public void impedanceDataAsComplex(double[] frequencies, Complex[] impedances, Complex[] impedanceWeights)
|
|
Regression procedure
|
|
Change the regression constraints
|
public void addNewConstraint(int parameterNumber, int direction, double boundary)
|
|
public void addNewConstraint(String parameterSymbol, int direction, double boundary)
|
|
public void removeDefaultConstraints()
|
|
public void removeAddedConstraints()
|
|
public void removeAllConstraints()
|
|
public void restoreDefaultConstraints()
|
|
Change the regression termination tolerance
|
public void resetTolerance(double tolerance)
|
|
Change the maximum number of regression iterations allowed
|
public void resetMaximumNumberOfIterations(int maximum)
|
|
Return all the results of the regression
|
public Vector<Object> getRegressionResults()
|
|
Get the best estimate values
|
public double[] getBestEstimates()
|
|
public double[] getStandardDeviations()
|
|
Plot the results
|
Set frequency axis plot option
|
public void setLog10Plot()
|
|
public void setLinearPlot()
|
|
Plot the impedance spectra
|
public Vector<Object> plotColeCole()
|
|
public Vector<Object> plotImpedanceMagnitudes()
|
|
public Vector<Object> plotImpedancePhases()
|
|
Plot the voltage spectra
|
public Vector<Object> plotVoltageMagnitudes()
|
|
public Vector<Object> plotVoltagePhases()
|
|
Write results to a file
|
Write results to a text file
|
public Vector<Object> printToTextFile(String fileName)
|
|
public Vector<Object> printToTextFile()
|
Write results to an Excel readable file
|
public Vector<Object> printToExcelFile(String fileName)
|
|
public Vector<Object> printToExcelFile()
|
The following methods in the class Impedance may be useful in building a user supplied circuit model where the user supplied class implementing the ImpedSpecModel interface may also extend Impedance.
|
Resistor impedance
|
public static Complex resistanceImpedance(double resistorValue)
|
|
Capacitor impedance
|
public static Complex capacitanceImpedance(double capacitorValue, double omega)
|
|
Inductor impedance
|
public static Complex inductanceImpedance(double inductorValue, double omega)
|
|
'Infinite' Warburg impedance
|
public static Complex infiniteWarburgImpedance(double sigma, double omega)
|
|
'Finite' Warburg impedance
|
public static Complex finiteWarburgImpedance(double sigma, double delta, double omega)
|
|
Constant phase element impedance
|
public static Complex constantPhaseElementImpedance(double sigma, double alpha, double omega)
|
|
Precompiled model circuit impedance
|
public static Complex
modelImpedance(double[] parameters, double omega, int modelNumber)
|
|
Impedances in series
|
public static Complex
impedanceInSeries(Complex impedance1, Complex impedance2)
|
|
public static Complex
impedanceInSeries(double impedance1, Complex impedance2)
|
|
public static Complex
impedanceInSeries(Complex impedance1, double impedance2)
|
|
public static Complex
impedanceInSeries(double impedance1, double impedance2)
|
|
public static Complex
rInSeriesWithC(double resistorValue, double capacitorValue, double omega)
|
|
public static Complex
rInSeriesWithL(double resistorValue, double inductorValue, double omega)
|
|
public static Complex
cInSeriesWithL(double capacitorValue, double inductorValue, double omega)
|
|
Impedances in parallel
|
public static Complex
impedanceInParallel(Complex impedance1, Complex impedance2)
|
|
public static Complex
impedanceInParallel(double impedance1, Complex impedance2)
|
|
public static Complex
impedanceInParallel(Complex impedance1, double impedance2)
|
|
public static Complex
impedanceInParallel(double impedance1, double impedance2)
|
|
public static Complex
rInParallelWithC(double resistorValue, double capacitorValue, double omega)
|
|
public static Complex
rInParallelWithL(double resistorValue, double inductorValue, double omega)
|
|
public static Complex
cInParallelWithL(double capacitorValue, double inductorValue, double omega)
|
|
List of precompiled model circuit components
|
public static String[ ]
modelComponents(int modelNumber)
|
|
Warburg coefficient, σ
|
public static double
warburgSigma(double electrodeArea, double oxidantDiffCoeff, double reductantDiffCoeff, double oxidantConcn, double reductantConcn, int electronsTransferred)
|
|
Parallel plate capacitance
|
public static double
parallelPlateCapacitance(double plateArea, double plateSeparation, double relativePermittivity)
|
|
public static double
parallelPlateCapacitance(double plateLength, double plateWidth, double plateSeparation, double relativePermittivity)
|
|
Coaxial cylinders - capacitance
|
public static double
coaxialCapacitance(double cylinderLength, double innerRadius, double outerRadius, double relativePermittivity)
|
|
Parallel wires - capacitance
|
public static double
parallelWiresCapacitance(double wireLength, double wireRadius, double wireSeparation, double relativePermittivity)
|
|
Parallel plates - inductance
|
public static double parallelPlateInductance(double plateLength, double plateWidth, double plateSeparation, double relativePermeability)
|
|
Coaxial cylinders - inductance
|
public static double
coaxialInductance(double cylinderLength, double innerRadius, double outerRadius, double relativePermbeability)
|
|
Parallel wires - inductance
|
public static double
parallelWiresInductance(double wireLength, double wireRadius, double wireSeparation, double relativePermbeability)
|
|
Magnitudes and phases
|
public static double
getMagnitude(Complex variable)
|
|
public static double
getPhaseRad(Complex variable)
|
|
public static double
getPhaseDeg(Complex variable)
|
|
Conversions
|
public static Complex
polarRad(double magnitude, double phaseRad)
|
|
public static Complex
polarDeg(double magnitude, double phaseDeg)
|
| public static double frequencyToRadialFrequency(double frequency) |
| public static double radialFrequencyToFrequency(double radial) |
CONSTRUCTORS
public ImpedSpecRegression()
Usage:
ImpedSpecRegression isr = new ImpedSpecRegression();
Creates an instance of ImpedSpecRegression.
public ImpedSpecRegression(String title)
Usage:
ImpedSpecRegression isr = new ImpedSpecRegression(title);
Creates an instance of ImpedSpecRegression. The argument title contains a title that will be displayed on plots and printed in the header of the output text file.
METHODS
ENTER THE CIRCUIT MODEL
A precompiled model/test circuit may be chosen or a user supplied model circuit may be entered
The non-linear regression procedure used requires initial estimates of the circuit parameters to be estimated plus estimates of how good you feel the initial estimates themselves are, i.e. initial step sizes. These are enetered through or calculated by these setModel methods.
Choose one of the precompiled circuit models
public void setModel(int modelNumber)
Usage:
isr.setModel(modelNumber);
This methods allows the selection of a precomplied model circuit. The available models are listed in ImpedSpecCircuitModels.pdf. The model circuits are listed in this pdf as:
- a model number (to be entered as the argument modelNumber);
- a list of the circuit parameter symbols as used in the input and output methods of this class;
- a diagram of the circuit
The values of the initial estimates of the model parameters are calculated by the method. If the user has a good idea of the probable values of the circuit parameters one of the methods listed immediately below, allowing the user to enter the initial estimates, is likely to be more appropriate, especially for a more complex circuit. If this method is used, the initial step sizes are set to 10% of the calculated initial estimates. See below for a method allowing user entered step sizes.
public void setModel(int modelNumber, double[ ] initialEstimates)
Usage:
isr.setModel(modelNumber, initialEstimates);
This methods allows the selection of a precomplied model circuit. The available models are listed in ImpedSpecCircuitModels.pdf. The model circuits are listed in this pdf as:
- a model number (to be entered as the argument modelNumber);
- a list of the circuit parameter symbols as used in the input and output methods of this class;
- a diagram of the circuit
The values of the initial estimates of the model parameters should be entered, in SI units, via the array of doubles, argument initialEstimates, and they should be in the same order as the list of parameter symbols referred to in (ii) above. If this method is used, the initial step sizes are set to 10% of the initial estimates. See immediately below for a method allowing user entered step sizes.
public void setModel(int modelNumber, double[ ] initialEstimates, double[ ] initialSteps)
Usage:
isr.setModel(modelNumber, initialEstimates, initialSteps);
This methods allows the selection of a precomplied model circuit. The available models are listed in ImpedSpecCircuitModels.pdf. The model circuits are listed in this pdf as:
- a model number (to be entered as the argument modelNumber);
- a list of the circuit parameter symbols as used in the input and output methods of this class;
- a diagram of the circuit
The values of the initial estimates of the model parameters should be entered, in SI units, via the array of doubles, argument initialEstimates, and the initial step sizes should be entered via the array of doubles, argument initialSteps, and they both should be in the same order as the list of parameter symbols referred to in (ii) above.
Enter a user supplied circuit model
public void setModel(ImpedSpecModel userModel, String[ ] symbols, double[ ] initialEstimates)
Usage:
isr.setModel(userModel, symbols, initialEstimates);
This method allows the user to enter their own circuit model, using the interface ImpedSpecModel, via the argument userModel [See Coding a user supplied circuit model]. The symbols, to be used in the output text file, for the model circuit parameters are entered via the array of Strings, argument symbols, in the order determined by the coding in userModel. The values of the initial estimates should be entered, in SI units, via the array of doubles, argument initialEstimates, in the same order as that of the symbols in symbol. If this method is used, the initial step sizes are set to 10% of the initial estimates. See immediately below for a method allowing user entered step sizes.
public void setModel(ImpedSpecModel userModel, String[ ] symbols, double[ ] initialEstimates, double[ ] initialSteps)
Usage:
isr.setModel(userModel, symbols, initialSteps);
This method allows the user to enter their own circuit model, using the interface ImpedSpecModel, via the argument userModel [See Coding a user supplied circuit model]. The symbols, to be used in the output text file, for the model circuit parameters are entered via the array of Strings, argument symbols, in the order determined by the coding in userModel. The values of the initial estimates and of the initial step sizes should be entered, in SI units, via the array of doubles, argument initialEstimates and the array of doubles, argument initialSteps, in the same order as that of the symbols in symbol.
Get the circuit parameter symbols and initial estimates
public double[] getInitialEstimates()
Usage:
initialEstimates = isr.getInitialEstimates();
Returns the entered or calculated initial estimates.
public String[] getCircuitComponents()
Usage:
circuitSymbols = isr.getCircuitComponents();
Returns the parameter symbols used in the selected or user entered model circuit.
Coding a user supplied circuit model
A class that extends the superclass Impedance and implements the interface ImpedSpecModel should be created. This class should contain a method named modelImpedance with the signature:
public Complex modelImpedance(double[ ] parameters, double omega)
This method should calculate and return the complex impedance of the user supplied circuit using the circuit parameter values passed through the argument, parameters, at the radial frequency passed through the argument, omega. The methods for calculating impedances, inherited from the superclass, Impedance and listed above, may be used in this method. A program demonstrating the use of a user supplied circuit is included in the Example Programs (Example Program Two).
Circuits coded in this manner may used as user models by both this class, ImpedSpecRegression, and the impedance spectroscopy simulation class, ImpedSpecSimulation.
ENTER THE EXPERIMENTAL DATA
The experimental data may be entered as one of the following:
- the magnitudes, Vtest, and phases, φ of the voltage across the test or model circuit as a function of frequency, ω [applied voltage and reference impedance must also be entered]
- the real and imaginary parts of the voltage across the test or model circuit as a function of frequency, ω [applied voltage and reference impedance must also be entered]
- the magnitudes and phases of the impedance of the test or model circuit as a function of frequency, ω
- the real and imaginary parts of the impedance of the test or model circuit as a function of frequency, ω.
SET THE REFERENCE IMPEDANCE
The reference impedance may be entered as a resistance or as a complex impedance. The reference impedance must be entered if the data is to be entered as the voltages measured across the test/model circuit. A reference impedance is not entered if the data is to be entered as the impedances of the test/model circuit.
public void setReferenceImpedance(double resistance)
Usage:
isr.setReferenceImpedance(resistance);
Sets the reference impedance to the resistance value, resistance.
public void setReferenceImpedance(double refRealZ, double refImagZ)
Usage:
isr.setReferenceImpedance(realZ, imagZ);
Sets the reference impedance to the complex impedance whose real part is realZ and whose real part is imagZ.
public void setReferenceImpedance(Complex referenceImpedance)
Usage:
isr.setReferenceImpedance(referenceImpedance);
Sets the reference impedance to the complex impedance referenceImpedance.
SET THE APPLIED VOLTAGE
The applied voltage must be entered if the data is to be entered as the voltages measured across the test/model circuit. An applied voltage is not entered if the data is to be entered as the impedances of the test/model circuit.
public void setAppliedVoltage(double appliedVoltage)
Usage:
isr.setAppliedVoltage(appliedVoltage);
Sets the applied voltage to the value appliedVoltage. This method is used if no weighting factors are to be entered for the regression. See immediately below for an appropriate method if a weighted regression is to be used.
public void setAppliedVoltage(double appliedVoltage, double appliedVoltageError)
Usage:
isr.setAppliedVoltage(appliedVoltage, appliedVoltageError);
Sets the applied voltage to the value appliedVoltage and sets the error in the applied voltage to the value appliedVoltageError.
This method allows the propagation of the correct weighting factors for the real and imaginary parts of the test/model circuit impedances if a weighted regression is to be used. If it is not entered and a weighted regression is used, the error in the appled voltage will be assumed to be zero.
ENTER THE EXPERIMENTAL DATA AS TEST/MODEL CIRCUIT VOLTAGES
As magnitudes and phases in degrees
public void voltageDataAsPhasorDeg(double[] frequencies, double[] voltageMagnitudes, double[] voltagePhasesDeg)
Usage:
isr.voltageDataAsPhasorRad(frequencies, voltageMagnitudes voltagePhasesDeg);
The experimental data may be entered, using this method, as the test/model circuit voltage magnitudes, Vtest [argument voltageMagnitudes], and phases in degrees, φ [argument voltagePhasesDeg], at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used an unweighted regression is performed by the data fitting methods.
public void voltageDataAsPhasorDeg(double[] frequencies, double[] voltageMagnitudes,double[] voltagePhasesDeg, double[] voltageMagWeights, double[] voltagePhaseWeights)
Usage:
isr.voltageDataAsPhasorDeg(frequencies, voltageMagnitudes voltagePhasesDeg, voltageMagWeights, voltagePhaseWeights);
The experimental data may be entered, using this method, as the test/model circuit voltage magnitudes, Vtest [argument voltageMagnitudes], the phases in degrees, φ [argument voltagePhasesDeg], the errors in the voltage magnitudes, [argument voltageMagweights], and the errors in the voltage phases, [argument voltagePhaseweights] at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used a weighted regression is performed by the data fitting methods. Ideally the errors should be the standard deviations of the measurements at each frequency.
As magnitudes and phases in radians
public void voltageDataAsPhasorRad(double[] frequencies, double[] voltageMagnitudes, double[] voltagePhasesRad)
Usage:
isr.voltageDataAsPhasorRad(frequencies, voltageMagnitudes, voltagePhasesRad);
The experimental data may be entered, using this method, as the test/model circuit voltage magnitudes, Vtest [argument voltageMagnitudes], and phases in radians, φ [argument voltagePhasesRad], at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used an unweighted regression is performed by the data fitting methods.
public void voltageDataAsPhasorRad(double[] frequencies, double[] voltageMagnitudes,double[] voltagePhasesRad, double[] voltageMagWeights, double[] voltagePhaseWeights)
Usage:
isr.voltageDataAsPhasorDeg(frequencies, voltageMagnitudes, voltagePhasesRad, voltageMagWeights, voltagePhaseWeights);
The experimental data may be entered, using this method, as the test/model circuit voltage magnitudes, Vtest [argument voltageMagnitudes], the phases in radians, φ [argument voltagePhasesRad], the errors in the voltage magnitudes, [argument voltageMagweights], and the errors in the voltage phases, [argument voltagePhaseweights] at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used a weighted regression is performed by the data fitting methods. Ideally the errors should be the standard deviations of the measurements at each frequency.
As the real and imaginary parts of the test/model circuit voltage
public void voltageDataAsComplex(double[] frequencies, double[] real,double[] imag)
Usage:
isr.voltageDataAsComplex(frequencies, real, imag);
The experimental data may be entered, using this method, as the test/model circuit complex voltage as its real part, [argument real], and its imaginary part [argument imag], at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used an unweighted regression is performed by the data fitting methods.
public void voltageDataAsComplex(double[] frequencies, double[] real,double[] imag, double[] realWeights, double[] imagWeights)
Usage:
isr.voltageDataAsComplex(frequencies, real, imag);
The experimental data may be entered, using this method, as the test/model circuit complex voltage as its real part [argument real], its imaginary part [argument imag], the error of the real part [argument realWeight] an the error of the imaginary part [argument imagWeight] at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used a weighted regression is performed by the data fitting methods. Ideally the errors should be the standard deviations of the measurements at each frequency.
As the complex test/model circuit voltage
public void voltageDataAsComplex(double[] frequencies, Complex[] voltages)
Usage:
isr.voltageDataAsComplex(frequencies, voltages);
The experimental data may be entered, using this method, as the test/model circuit complex voltage [argument voltage] at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used a unweighted regression is performed by the data fitting methods. See class Complex for this library's conventions and methods of handling complex numbers.
public void voltageDataAsComplex(double[] frequencies, Complex[] voltages, Complex[] voltageWeights)
Usage:
isr.voltageDataAsComplex(frequencies, voltages);
The experimental data may be entered, using this method, as the test/model circuit complex voltage [argument voltage] and the error of the complex voltage [argument voltageWeights] at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used a weighted regression is performed by the data fitting methods. Ideally the errors should be the standard deviations of the measurements at each frequency. See class Complex for this library's conventions and methods of handling complex numbers.
ENTER THE EXPERIMENTAL DATA AS TEST/MODEL CIRCUIT IMPEDANCES
As magnitudes and phases in degrees
public void impedanceDataAsPhasorDeg(double[] frequencies, double[] impedanceMagnitudes, double[] impedancePhasesDeg)
Usage:
isr.impedanceDataAsPhasorRad(frequencies, impedanceMagnitudes impedancePhasesDeg);
The experimental data may be entered, using this method, as the test/model circuit impedance magnitudes, Vtest [argument impedanceMagnitudes], and phases in degrees, φ [argument impedancePhasesDeg], at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used an unweighted regression is performed by the data fitting methods.
public void impedanceDataAsPhasorDeg(double[] frequencies, double[] impedanceMagnitudes,double[] impedancePhasesDeg, double[] impedanceMagWeights, double[] impedancePhaseWeights)
Usage:
isr.impedanceDataAsPhasorDeg(frequencies, impedanceMagnitudes impedancePhasesDeg, impedanceMagWeights, impedancePhaseWeights);
The experimental data may be entered, using this method, as the test/model circuit impedance magnitudes, Vtest [argument impedanceMagnitudes], the phases in degrees, φ [argument impedancePhasesDeg], the errors in the impedance magnitudes, [argument impedanceMagweights], and the errors in the impedance phases, [argument impedancePhaseweights] at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used a weighted regression is performed by the data fitting methods. Ideally the errors should be the standard deviations of the measurements at each frequency.
As magnitudes and phases in radians
public void impedanceDataAsPhasorRad(double[] frequencies, double[] impedanceMagnitudes, double[] impedancePhasesRad)
Usage:
isr.impedanceDataAsPhasorRad(frequencies, impedanceMagnitudes, impedancePhasesRad);
The experimental data may be entered, using this method, as the test/model circuit impedance magnitudes, Vtest [argument impedanceMagnitudes], and phases in radians, φ [argument impedancePhasesRad], at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used an unweighted regression is performed by the data fitting methods.
public void impedanceDataAsPhasorRad(double[] frequencies, double[] impedanceMagnitudes,double[] impedancePhasesRad, double[] impedanceMagWeights, double[] impedancePhaseWeights)
Usage:
isr.impedanceDataAsPhasorDeg(frequencies, impedanceMagnitudes, impedancePhasesRad, impedanceMagWeights, impedancePhaseWeights);
The experimental data may be entered, using this method, as the test/model circuit impedance magnitudes, Vtest [argument impedanceMagnitudes], the phases in radians, φ [argument impedancePhasesRad], the errors in the impedance magnitudes, [argument impedanceMagweights], and the errors in the impedance phases, [argument impedancePhaseweights] at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used a weighted regression is performed by the data fitting methods. Ideally the errors should be the standard deviations of the measurements at each frequency.
As the real and imaginary parts of the test/model circuit impedance
public void impedanceDataAsComplex(double[] frequencies, double[] real,double[] imag)
Usage:
isr.impedanceDataAsComplex(frequencies, real, imag);
The experimental data may be entered, using this method, as the test/model circuit complex impedance as its real part, [argument real], and its imaginary part [argument imag], at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used an unweighted regression is performed by the data fitting methods.
public void impedanceDataAsComplex(double[] frequencies, double[] real,double[] imag, double[] realWeights, double[] imagWeights)
Usage:
isr.impedanceDataAsComplex(frequencies, real, imag);
The experimental data may be entered, using this method, as the test/model circuit complex impedance as its real part [argument real], its imaginary part [argument imag], the error of the real part [argument realWeight] an the error of the imaginary part [argument imagWeight] at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used a weighted regression is performed by the data fitting methods. Ideally the errors should be the standard deviations of the measurements at each frequency.
As the complex test/model circuit impedance
public void impedanceDataAsComplex(double[] frequencies, Complex[] impedances)
Usage:
isr.impedanceDataAsComplex(frequencies, impedances);
The experimental data may be entered, using this method, as the test/model circuit complex impedance [argument impedance] at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used a unweighted regression is performed by the data fitting methods. See class Complex for this library's conventions and methods of handling complex numbers.
public void impedanceDataAsComplex(double[] frequencies, Complex[] impedances, Complex[] impedanceWeights)
Usage:
isr.impedanceDataAsComplex(frequencies, impedances);
The experimental data may be entered, using this method, as the test/model circuit complex impedance [argument impedance] and the error of the complex impedance [argument impedanceWeights] at the applied frequencies, ω [argument frequencies] entered in Hz. If this method is used a weighted regression is performed by the data fitting methods. Ideally the errors should be the standard deviations of the measurements at each frequency. See class Complex for this library's conventions and methods of handling complex numbers.
REGRESSION PROCEDURE
The superclasses's non-linear regression is used with the frequencies as the independent variable and the real parts and the imaginary parts of the test circuit complex impedance as the dependent variables. This procedure uses a Nelder and Mead simplex based constrained minimisation of either the sum of squares of the residuals (unweighted data) or chi-square (weighted data). See the Regression class for details of the Nelder and Mead non-linear regression procedure. The regression procedure is called twice; firstly with the user supplied or class calculated initial estimates, secondly with the best estimates from the first regression call as the initial estimates. The default constraints are described below and may be altered.
Change or add to the regression constraints
This class's default non-linear regression procedure uses a constrained minimisation of the sum of squares of the residuals. All the circuit parameters, i.e. resistances R, capacitances C, inductances L, Warburg coefficients σ and δ and constant phase element coefficients, σ and α are constrained to be equal to or greater than 0. In addition the constant phase element power, α is constrained to be less than or equal to 1. These constraints may be removed, altered or supplemented with further constraints.
public void addNewConstraint(int parameterNumber, int direction, double boundary)
public void addNewConstraint(String parameterSymbol, int direction, double boundary)
Usage:
isr.addNewConstraint(parameter, direction, boundary);
The method allows the addition of further constraints.
The first argument parameter is the parameter to be constrained. It may be entered as an integer indicating the parameter or as the symbol representing the parameter, e.g. "C1", in the chosen or user model description. If the integer format is used the order of parameters is that listed in the model circuits pdf or in the user model coding. The parameter list starts at 0 and not at 1, i.e. the integer indicating the first parameter is 0.
The second argument direction indicates the region of the constraint. A value of 1 indicates that the constraint should be applied for values greater than the third argument, boundary. A value of -1 indicates that the constraint should be applied for values less than the third argument, boundary. If the added constraint is incompatible with a default constraint the added constraint overrides the default constraint.
public void removeDefaultConstraints()
Usage:
isr.removeDefaultConstraints();
The method removes all the default constraints.
public void restoreDefaultConstraints()
Usage:
isr.restoreDefaultConstraints();
The method restores all the default constraints.
public void removeAddedConstraints()
Usage:
isr.removeAddedConstraints();
The method removes all added constraints.
public void removeAllConstraints()
Usage:
isr.removeAllConstraints();
The method removes all default and added constraints.
Change the regression termination tolerance
public void resetTolerance(double tolerance)
Usage:
isr.resetTolerance(tolerance);
This method allows the user to reset the tolerance [argument tolerance] used to determine when the regression procedure has minimised the sum of squares of the residuals. The default value is 1 x 10-9. See Regression class - convergence tests for a discussion of the regression's minimisation termination procedure.
Change the maximum number of regression iterations allowed
public void resetMaximumNumberOfIterations(int maximum)
Usage:
isr.resetMaximumNumberOfIterations(maximum);
This method allows the user to reset the maximum number of iterations [argument maximum] allowed in the regression procedure. The default value is 10000.
Return all the results of the regression
IT IS STRONGLY ADVISED THAT THE RESULTS OF THE REGESSION ARE ALSO DISPLAYED AS A PLOT (METHODS BELOW) FOR VISUAL INSPECTION OF THE GOODNESS OF THE FIT.
public Vector<Object> getAllRegressionResults()
Usage:
Vector<Object> results = isr.getRegressionResults();
This method performs the regression, if it has not already been performed, and returns a Vector whose elements contain the following data:
| element 0: | number of of data points, n, i.e. number of frequencies | [as an Integer] |
| element 1: | number of parameters in the model, p | [as an Integer] |
| element 2: | degrees of freedom, ν, i.e. n − p | [as an Integer] |
| element 3: | circuit parameter symbols | [as an array of Strings] |
| element 4: | initial estimates | [as an array of doubles] |
| element 5: | initial step sizes | [as an array of doubles] |
| element 6: | best estimates returned by the regression procedure | [as an array of doubles] |
| element 7: | standard deviations of the best estimate. See Standard deviations (below) for a note of caution on interpreting these estimated standard deviations | [as an array of doubles] |
| element 8: | coefficients of variation of the best estimates, i.e.
(100 x standard deviation) / (best estimate) | [as an array of doubles] |
| element 9: | correlation coefficients of the best estimates | [as a two dimensional array of doubles] |
| element 10: | the gradients on the regression surface immediately before the minimum
calculated numerically for each parameter | [as an array of doubles] |
| element 11: | the gradients on the regression surface immediately after the minimum
calculated numerically for each parameter | [as an array of doubles] |
| element 12: | sum of squares of the residuals | [as a Double] |
| element 13: | reduced sum of squares of the residuals, i.e.
(sum of squares of the residuals)/(degrees of freedom) | [as a Double] |
| element 14: | chiSquare, i.e.
sum of the squares of the weighted residual | [as a Double if weights were provided, null if no weights] |
| element 15: | reduced chiSquare
| [as a Double if weights were provided, null if no weights] |
| element 16: | number of iterations taken by the regression procedure
| [as an Integer] |
| element 17: | maximum number of iterations allowed
| [as an Integer] |
| element 18: | mode of data entry, e.g. as real and imaginary parts of the impedance
| [as a String] |
| element 19: | frequencies (Hz)
| [as an array of doubles] |
| element 20: | log10[frequencies/Hz]
| [as an array of doubles] |
| element 21: | radial frequencies
| [as an array of doubles] |
| element 22: | log10[[radial frequencies]
| [as an array of doubles] |
| element 23: | experimental voltage magnitudes
| [as an array of doubles] |
| element 24: | experimental voltage phases as radians
| [as an array of doubles] |
| element 25: | experimental voltage phases as degrees
| [as an array of doubles] |
| element 26: | experimental complex voltages
| [as an array of Complex] |
| element 27: | real parts of the experimental voltages
| [as an array of doubles] |
| element 28: | imaginary parts of the experimental voltages
| [as an array of doubles] |
| element 29: | real parts of the experimental impedances
| [as an array of doubles] |
| element 30: | imaginary parts of the experimental impedances
| [as an array of doubles] |
| element 31: | calculated values of the real part of the impedances | [as an array of doubles] |
| element 32: | calculated values of the imaginary part of the impedances | [as an array of doubles] |
| element 33: | Real[impedance] residuals, i.e.
experimental Real[impedance] - calculated Real[impedance] | [as an array of doubles] |
| element 34: | Imag[impedance] residuals, i.e.
experimental Imag[impedance] - calculated Imag[impedance] | [as an array of doubles] |
| element 35: | entered weights for the first data array, ie.
for Real[impedance], complex impedance or magnitude | [as an array of doubles if weights were provided, null if no weights ] |
| element 36: | entered weights for the second data array, ie.
for Imag[impedance] or phase, null if impedance was entered as a Complex | [as an array of doubles if weights were provided, null if no weights ] |
| element 37: | weights used in the regression for Real[impedance], if weights have been entered
if the weights were not entered as Real[impedance] weights, the used Real[impedance] weights were calculated using the ErrorProp and ComplexErrorProp error propagation classes | [as an array of doubles if weights were provided, null if no weights ] |
| element 38: | weights used in the regression for Imag[impedance], if weights have been entered
if the weights were not entered as Imag[impedance] weights, the used Imag[impedance] weights were calculated using the ErrorProp and ComplexErrorProp error propagation classes | [as an array of doubles if weights were provided, null if no weights ] |
| element 39: | calculated impedances | [as an array of Complex ] |
| element 40: | real parts of the calculated voltages | [as an array of doubles ] |
| element 41: | imaginary parts of the calculated voltages | [as an array of doubles ] |
| element 42: | calculated voltages | [as an array of Complex ] |
| element 43: | magnitudes of the calculated voltages | [as an array of doubles ] |
| element 44: | phases (as radians) of the calculated voltages | [as an array of doubles ] |
| element 45: | phases (as degrees) of the calculated voltages | [as an array of doubles ] |
Get the best estimate values and their standard deviations
IT IS STRONGLY ADVISED THAT THE RESULTS OF THE REGESSION ARE ALSO DISPLAYED AS A PLOT (METHODS BELOW) FOR VISUAL INSPECTION OF THE GOODNESS OF THE FIT.
public double[] getBestEstimates()
Usage:
bestEstimates = isr.getBestEstimates();
Returns the values of the best estimates for the test/model circuit parameters obtained from the regression.
public double[] getStandardDeviations()
Usage:
standDev = isr.getStandardDeviations();
Returns the estimates of the standard deviations of the best estimates for the test/model circuit parameters obtained from the regression. CAUTION: The standard deviations are calculated from a variance-covariance matrix obtained as the inverse of the Hessian matrix of numerically calculated second partial differentials of either the chi square or sum of squares of the residuals with respect to all pairs of parameters, i.e. assuming that the model is linear in the region of the minimum. As this may not be true great caution should be exercised in viewing the standard deviations. An examination of the pre- and post-minimum gradients (see returned Vector described immediately above) is recommended. If the Hessian matrix cannot be inverted an array of Double.NaN is returned. If a negative covariance is calculated for a parameter Double.NaN is returned as the corresponding standard deviation.
PLOT THE RESULTS OF THE REGRESSION
The regression results may be plotted as:
- Cole-Cole plots
- impedance magnitude against frequency
- impedance phase against frequency
- voltage magnitude against frequency
- voltage phase against frequency
The default frequency scale option in the plotting method is to plot the frequency axis on a log10 scale as a log frequency scale is the standard and recommended scale in impedance spectroscopy. This scale may be changed to a linear scale if required.
Reset the log/linear scale option
public void setLinearPlot()
Usage:
isr.setLinearPlot();
This method resets the graphs' frequency axis from a log to the base 10 scale to a linear scale.
public void setLog10Plot()
Usage:
isr.setLog10Plot();
This method resets the graphs' frequency axis from a linear scale to a log to the base 10 scale.
Plot the impedance spectra
Cole-Cole plots
public void plotColeCole()
Usage:
isr.plotColeCole();
or:
Vector<Object> results = isr.plotColeCole();
This method carries out the regression, if not already done, and displays a Cole-Cole plot, i.e. a plot of the imaginary parts of the test/model circuit complex impedance against the real parts of the complex impedance for both the experimentally determined values and those calculated using the best fit estimates. The method also returns the Vector of all the regression results as described in the documentation of the getRegressionResults method
Impedance magnitude plots
public void plotImpedanceMagnitudes()
Usage:
isr.plotImpedanceMagnitudes();
or:
Vector<Object> results = isr.plotImpedanceMagnitudes();
This method carries out the regression, if not already done, and displays a plot of the magnitudes of the test/model circuit impedance against the frequency in Hz for both the experimentally determined values and those calculated using the best fit estimates. The method also returns the Vector of all the regression results as described in the documentation of the getRegressionResults method
Impedance phase plots
public void plotImpedancePhases()
Usage:
isr.plotImpedancePhases();
or:
Vector<Object> results = isr.plotImpedancePhases();
This method carries out the regression, if not already done, and displays a plot of the phases, in degrees, of the test/model circuit impedance against the frequency in Hz for both the experimentally determined values and those calculated using the best fit estimates. The method also returns the Vector of all the regression results as described in the documentation of the getRegressionResults method
Plot the voltage spectra
Voltage magnitude plots
public void plotVoltageMagnitudes()
Usage:
isr.plotVoltageMagnitudes();
or:
Vector<Object> results = isr.plotVoltageMagnitudes();
This method carries out the regression, if not already done, and displays a plot of the magnitudes of the voltage appearing across the test/model circuit against the frequency in Hz for both the experimentally determined values and those calculated using the best fit estimates. The method also returns the Vector of all the regression results as described in the documentation of the getRegressionResults method
Voltage phase plots
public void plotVoltagePhases()
Usage:
isr.plotVoltagePhases();
or:
Vector<Object> results = isr.plotVoltagePhases();
This method carries out the regression, if not already done, and displays a plot of the phases, in degrees, of the voltage appearing across the test/model circuit against the frequency in Hz for both the experimentally determined values and those calculated using the best fit estimates. The method also returns the Vector of all the regression results as described in the documentation of the getRegressionResults method
WRITE RESULTS TO A FILE
IT IS STRONGLY ADVISED THAT THE RESULTS OF THE REGESSION ARE ALSO DISPLAYED AS A PLOT (METHODS BELOW) FOR VISUAL INSPECTION OF THE GOODNESS OF THE FIT.
Write to a .txt file
public void printToTextFile(String fileName)
Usage:
isr.printToTextFile(fileName);
or:
Vector<Object> results = isr.printToTextFile(fileName);
This method carries out the regression, if not already done, and prints to a text file, named fileName, the following:
- program title
- file name
- time and date that the file was created
- circuit parameters
- best estimates of the parameter values
- standard deviations of the best estimates of the parameter values
- coefficients of variation of the best estimates of the parameter values
- pre-minimum gradients
- post-minimum gradients
- initial estimates of the parameter values
- initial step sizes
- sum of squares of the Real[Z] and Imag[Z] residuals
- reduced sum of squares of the Real[Z] and Imag[Z] residuals
- degrees of freedom
- chi square, if weighted data entered
- reduced chi square, if weighted data entered
- number of iterations taken in the first regression
- number of iterations taken in the second regression
- maximum number of iterations allowed in each regression
- applied voltage, if entered
- reference impedance, if entered
- frequencies in Hz
- experimental real parts of the test/model circuit impedances
- experimental imaginary parts of the test/model circuit impedances
- calculated real parts of the test/model circuit impedances using the best estimate values
- calculated imaginary parts of the test/model circuit impedances using the best estimate values
- the experimental data as entered
The method also returns the Vector of all the regression results as described in the documentation of the getRegressionResults method
public void printToTextFile()
Usage:
isr.printToTextFile();
or:
Vector<Object> results = isr.printToTextFile();
This method carries out the regression, if not already done, and prints to a text file, named ImpedSpecRegressionOutputn.txt, the data listed above for method printToTextFile(fileName). The integer n in the file name starts at 1 and is incremented by 1 every time the method is called without the previous output file being removed from the working directory.
The method also returns the Vector of all the regression results as described in the documentation of the getRegressionResults method
Write to a Excel readable file
public void printToExcelFile(String fileName)
Usage:
isr.printToExcelFile(fileName);
or:
Vector<Object> results = isr.printToExcelFile(filename);
This method carries out the regression, if not already done, and prints to a file, named fileName.xls, the data listed above for method printToTextFile(fileName). This file is in a format that facilitates the display of the data columns as Excel sheet columns when this file is opened with Microsoft Excel.
The method also returns the Vector of all the regression results as described in the documentation of the getRegressionResults method
public void printToExcelFile()
Usage:
isr.printToExcelFile();
or:
Vector<Object> results = isr.printToExcelFile();
This method carries out the regression, if not already done, and prints to a file, named ImpedSpecRegressionOutputn.xls, the data listed above for method printToTextFile(fileName). This file is in a format that facilitates the display of the data columns as Excel sheet columns when this file is opened with Microsoft Excel. The integer n in the file name starts at 1 and is incremented by 1 every time the method is called without the previous output file being removed from the working directory. This file can be read by MS Excel maintaining the data columns as Excel sheet columns.
The method also returns the Vector of all the regression results as described in the documentation of the getRegressionResults method
METHODS IN THE CLASS, Impedance
These may be useful in building a user supplied circuit model. The user supplied class implementing the interface ImpedSpecModel may also extend Impedance.
Resistor impedance
public static Complex resistanceImpedance(double resistorValue)
Usage:
imped = Impedance.resistanceImpedance(resistorValue);
Returns the impedance, Z, of a resistor, R [resitorValue entered in ohms], as a complex impedance:
Z = R + j0
Capacitor impedance
public static Complex capacitanceImpedance(double capacitorValue, double omega)
Usage:
imped = Impedance.capacitanceImpedance(capacitorValue, omega);
Returns the complex impedance, Z, of a capacitor, C [CapacitorValue entered in farads] at a radial frequency ω [omega]:
Z = 0 − j/Cω
Inductor impedance
public static Complex inductanceImpedance(double inductorValue, double omega)
Usage:
imped = Impedance.inductanceImpedance(inductorValue, omega);
Returns the complex impedance, Z, of a inductor, L [inductorValue entered in henries] at a radial frequency ω [omega]:
Z = 0 + jLω
'Infinite' Warburg impedance
public static Complex infiniteWarburgImpedance(double sigma, double omega)
Usage:
imped = Impedance.infiniteWarburgImpedance(sigma, omega);
Returns the Warburg impedance, Z, for an infinite diffusion layer and a constant, σ [sigma], at a radial frequency ω [omega]:
Z = σ/ω0.5 − jσ/ω0.5
See also Warburg coefficient, σ.
'Finite' Warburg impedance
public static Complex finiteWarburgImpedance(double sigma, double delta, double omega)
Usage:
imped = Impedance.finiteWarburgImpedance(sigma, delta, omega);
Returns the Warburg impedance, Z, for a finite diffusion layer and constants, σ [sigma] and δ [delta], at a radial frequency ω [omega]:
Z = σ/ω0.5(1 − j)tanh[δ(jω)0.5]
The parameter, δ, equals d/D-0.5 where d is the diffusion layer thickness and D is the relevant diffusion coefficient. The full finite Warburg impedance is the series combination:
Zfull = σo/ω0.5(1 − j)tanh[δo(jω)0.5] + σr/ω0.5(1 − j)tanh[δr(jω)0.5]
where the subscripts refer to the oxidant and reductant species respectively.
Constant phase element impedance
public static Complex constantPhaseElementImpedance(double sigma, double alpha, double omega)
Usage:
imped = Impedance.constantPhaseElementImpedance(sigma, alpha, omega);
Returns the impedance, Z, of a Constant Phase Element with constants, σ [sigma] and α [alpha], at a radial frequency ω [omega]:
Z = σ(jω)−α
Precompiled model circuit impedance
public static Complex
modelImpedance(double[] parameters, double omega, int modelNumber)
Usage:
imped = Impedance.modelImpedance(sigma, alpha, omega);
Returns the complex impedance of a designated model chosen from the list of precompiled circuit models at a radial frequency ω [omega]. The model number is entered as the argument, modelNumber, and the circuit parameters must be entered through the argument parameters in the same order as the list of parameter symbols to be found after the model number in ImpedSpecCircuitModels.pdf
Impedances in series
|
public static Complex
impedanceInSeries(Complex impedance1, Complex impedance2)
public static Complex
impedanceInSeries(double impedance1, Complex impedance2)
public static Complex
impedanceInSeries(Complex impedance1, double impedance2)
public static Complex
impedanceInSeries(double impedance1, double impedance2)
Usage:
imped = Impedance.impedanceInSeries(impedance1, impedance1);
Returns the complex impedance of a two impedances [arguments impedance1 and impedance2] in series. The impedances impedance1 and impedance2 may be complex or real (resistance).
public static Complex
rInSeriesWithC(double resistorValue, double capacitorValue, double omega)
Usage:
imped = Impedance.rInSeriesWithC(resistorValue, capacitorValue, omega);
Returns the complex impedance, at a radial frequency ω [argument omega], of a resistor [argument resistorValue (ohms)] in series with a capacitor [argument resistorValue (farads)].
public static Complex
rInSeriesWithL(double resistorValue, double inductorValue, double omega)
Usage:
imped = Impedance.rInSeriesWithL(resistorValue, inductorValue, omega);
Returns the complex impedance, at a radial frequency ω [argument omega], of a resistor [argument resistorValue (ohms)] in series with an inductor [argument inductorValue (henries)].
public static Complex
cInSeriesWithL(double capacitorValue, double inductorValue, double omega)
Usage:
imped = Impedance.cInSeriesWithL(capacitorValue, inductorValue, omega);
Returns the complex impedance, at a radial frequency ω [argument omega], of a capacitor [argument capacitorValue (farads)] in series with an inductor [argument inductorValue (henries)].
Impedances in parallel
|
public static Complex
impedanceInParallel(Complex impedance1, Complex impedance2)
public static Complex
impedanceInParallel(double impedance1, Complex impedance2)
public static Complex
impedanceInParallel(Complex impedance1, double impedance2)
public static Complex
impedanceInParallel(double impedance1, double impedance2)
Usage:
imped = Impedance.impedanceInParallel(impedance1, impedance1);
Returns the complex impedance of a two impedances [arguments impedance1 and impedance2] in parallel. The impedances impedance1 and impedance2 may be complex or real (resistance).
public static Complex
rInParallelWithC(double resistorValue, double capacitorValue, double omega)
Usage:
imped = Impedance.rInParallelWithC(resistorValue, capacitorValue, omega);
Returns the complex impedance, at a radial frequency ω [argument omega], of a resistor [argument resistorValue (ohms)] in parallel with an capacitor [argument capacitorValue (farads)].
public static Complex
rInParallelWithL(double resistorValue, double inductorValue, double omega)
Usage:
imped = Impedance.rInParallelWithL(resistorValue, inductorValue, omega);
Returns the complex impedance, at a radial frequency ω [argument omega], of a resistor [argument resistorValue (ohms)] in parallel with an inductor [argument inductorValue (henries)].
public static Complex
cInParallelWithL(double capacitorValue, double inductorValue, double omega)
Usage:
imped = Impedance.cInParallelWithL(capacitorValue, inductorValue, omega);
Returns the complex impedance, at a radial frequency ω [argument omega], of a capacitor [argument capacitorValue (farads)] in parallel with an inductor [argument inductorValue (henries)].
List of precompiled model circuit components
|
public static String[ ] modelComponents(int modelNumber)
Usage:
symbols = Impedance.modelComponents(modelNumber);
Returns an array of the parameter symbols, as listed in ImpedSpecCircuitModels.pdf, for a circuit selected from the range of precompiled circuit models. The model number is entered via the argument modelNumber.
Warburg Coefficient, σ
public static double
warburgSigma(double electrodeArea, double oxidantDiffCoeff, double reductantDiffCoeff, double oxidantConcn, double reductantConcn, int electronsTransferred)
Usage:
cap = Impedance.warburgSigma(electrodeArea, oxidantDiffCoeff, reductantDiffCoeff, oxidantConcn, reductantConcn, electronsTransferred);
Returns the warburg coefficient, σ,
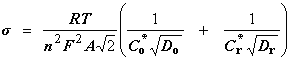
of elecrtode area, A square metres, [argument electrodeArea], oxidant diffusion coefficient, Do square metres per second, [argument oxidantDiffCoeff], reductant diffusion coefficient, Dr square metres per second, [argument reductantDiffCoeff], oxidant concentration at the electrode surface, C*o moles per cubic metre, [argument oxidantConcn], reductant concentration at the electrode surface, C*r moles per cubic metre, [argument reductantConcn] and the number of electrons transferred in the electrochemical reaction,
nr, [argument electronsTransferred].
Parallel Plate Capacitance
The plate area may be entered as an area or, additionally for rectangular plates, as a length and a width.
public static double parallelPlateCapacitance(double plateArea, double plateSeparation, double relativePermittivity)
Usage:
cap = Impedance.parallelPlateCapacitance(plateArea, plateSeparation, relativePermittivity);
Returns the capacitance, C in farads,
C = Aεoεr/d
of a parallel plate capacitor of plate area, A square metres, [argument plateArea], plate separation d metres, [argument plateArea] and dielectric relative electrical permittivity,
εr [argument relativePermittivity]. See classes
Water for the relative permittivity of water. Plate edge effects are ignored.
public static double parallelPlateCapacitance(double plateLength, double plateWidth, double plateSeparation, double relativePermittivity)
Usage:
cap = Impedance.parallelPlateCapacitance(plateLength, plateWidth, plateSeparation, relativePermittivity);
Returns the capacitance, C in farads,
C = lwεoεr/d
of a parallel plate capacitor of plate length, l metres, [argument plateLength], plate width, w metres, [argument plateWidth], plate separation d metres, [argument plateArea] and dielectric relative electrical permittivity,
εr [argument relativePermittivity]. See classes
Water for the relative permittivity of water. Plate edge effects are ignored.
Coaxial Cylinders - Capacitance
public static double
coaxialCapacitance(double cylinderLength, double innerRadius, double outerRadius, double relativePermittivity)
Usage:
cap = Impedance.coaxialCapacitance(cylinderLength, innerRadius, outerRadius, relativePermittivity);
Returns the capacitance, C in farads, of two coaxial cylinders,
C = 2lπεoεr/ln(router/router)
where l is the length of the cylinders in metres [argument cylinderLength], rinner is the radius from the coaxial centre point to the outer surface of the inner cylinder in metres [argument innerRadius], router is the radius from the coaxial centre point to the inner surface of the outer cylinder in metres[argument outerRadius] and εr is relative electrical permittivity of the dielectric between the inner and outer cylinders
[argument relativePermittivity]. Cylinder end effects are ignored.
Parallel Wires - Capacitance
public static double
parallelWiresCapacitance(double wireLength, double wireRadius, double wireSeparation, double relativePermittivity)
Usage:
cap = Impedance.parallelWiresCapacitance(wireLength, wireRadius, wireSeparation, relativePermittivity);
Returns the capacitance, C in farads, of two parallel wires,
C = lπεoεr/ln((d - r)/r)
where l is the length of the wires in metres [argument wireLength], r is the radius of the wires in metres [argument wiresRadius], d is the separation distance of the wires, measured from the centres of the wires, in metres [argument wireSeparation] and εr is relative electrical permittivity of the dielectric surrounding the wires [argument relativePermittivity]. It is assumed that the wires have identical radii and that the this radius is much smaller than the distance between the wires (no polarisation effects are considered) and wire end effects are ignored.
Parallel Plates - Inductance
public static double parallelPlateInductance(double plateLength, double plateWidth, double plateSeparation, double relativePermeability)
Usage:
ind = Impedance.parallelPlateInductance(plateLength, plateWidth, plateSeparation, relativePermeability);
Returns the inductance, L in henries,
C = ldμoμr/w
of a parallel plates of plate length, l metres, [argument plateLength], plate width, w metres, [argument plateWidth], plate separation d metres, [argument plateArea] and μr is relative magnetic permeability of the material between the plates
[argument relativePermeability]. Plate edge effects are ignored.
Coaxial Cylinders - Inductance
public static double
coaxialInductance(double cylinderLength, double innerRadius, double outerRadius, double relativePermeability)
Usage:
ind = Impedance.coaxialInductance(cylinderLength, innerRadius, outerRadius, relativePermeability);
Returns the capacitance, L in henrys, of two coaxial cylinders,
L = lμoμr
ln(router/router)/(2π)
where l is the length of the cylinders in metres [argument cylinderLength], rinner is the radius from the coaxial centre point to the outer surface of the inner cylinder in metres [argument innerRadius], router is the radius from the coaxial centre point to the inner surface of the outer cylinder in metres[argument outerRadius] and μr is relative magnetic permeability of the material between the inner and outer cylinders
[argument relativePermeability]. Cylinder end effects are ignored.
Parallel Wires - Inductance
public static double
parallelWiresInductance(double wireLength, double wireRadius, double wireSeparation, double relativePermeability)
Usage:
ind = Impedance.parallelWiresInductance(wireLength, wireRadius, wireSeparation, relativePermeability);
Returns the capacitance, L in henrys, of two parallel wires,
L = lμoμrln((d - r)/r)/π
where l is the length of the wires in metres [argument wireLength], r is the radius of the wires in metres [argument wiresRadius], d is the separation distance of the wires, measured from the centres of the wires, in metres [argument wireSeparation] and μr is relative magnetic permeability of the material surrounding the wires [argument relativePermeability]. It is assumed that the wires have identical radii and that the this radius is much smaller than the distance between the wires (no polarisation effects are considered) and wire end effects are ignored.
Magnitudes and phases
public static double
getMagnitude(Complex variable)
Usage:
mag = Impedance.getMagnitude(complexVariable);
Returns the modulus, i.e. the magnitude, of a complex variable [complexVariable].
public static double
getPhaseRad(Complex variable)
Usage:
phaseRadians = Impedance.getPhaseRad(complexVariable);
Returns the argument, i.e. the phase, in radians, of a complex variable [complexVariable].
public static double
getPhaseDeg(Complex variable)
Usage:
phaseDegrees = Impedance.getPhaseDeg(complexVariable);
Returns the argument, i.e. the phase, in degrees, of a complex variable [complexVariable].
Conversions
public static Complex
polarRad(double magnitude, double phaseRad)
Usage:
complexVariable = Impedance.polarRad(magnitude, phaseRadians);
Converts the phasor of magnitude, magnitude, and phase in radians, phaseRadians, to the rectangular complex variable, complexVariable,
magnitude.cos(phaseRadians) + j.magnitude.sin(phaseRadians).
public static Complex
polarDeg(double magnitude, double phaseDeg)
Usage:
complexVariable = Impedance.polarDeg(magnitude, phaseDegrees);
Converts the phasor of magnitude, magnitude, and phase in degrees, phaseDegrees, to the rectangular complex variable, complexVariable,
magnitude.cos(2.π.phaseDegrees/180) + j.magnitude.sin(2.π.phaseDegrees/180).
Frequency (Hz) to radial frequency
public static double frequencyToRadialFrequency(double freq)
Usage:
radial =
Fmath.frequencyToRadialFrequency(freq);
Converts the argument, freq, a frequency in Hz, to
the corresponding radial frequency and returns that value in radians per second.
Radial frequency to frequency
public static double radialfrequencyToFrequency(double rad)
Usage:
freq =
Fmath.radialFrequencyToFrequency(rad);
Converts the argument, rad, a radial frequency in radians per second, to
the corresponding frequency and returns that value in Hz.
EXAMPLE PROGRAMS
Example Program One
This program demonstrates the fitting of data to a model incorporating a constant phase element (Q1), model number 26,
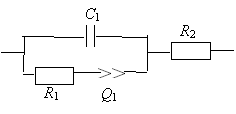
from the range of precompliled circuit models.
The data is contaminated with noise at a level of ~0.5%. This program also demonstrates the use of the FileChooser class in selecting a data file. The data file, ISRoneData.txt, lists:
- data title
- applied voltage
- reference impedance
- number of frequencies at which a measurement was made
- a table of the data as rows of frequency in Hz, magnitude of the voltage across the test/model circuit, Vtest, and the phase of the voltage across the test/model circuit, φ.
Example Program One source code: ExampleProgramOneImpedRegr.java
Example Program Two
This program demonstrates the fitting of data to a user supplied model/test circuit
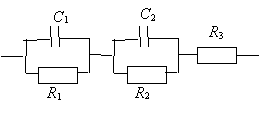
using the interface ImpedSpecModel.
The data is contaminated with noise at a level of ~0.5%. This program also demonstrates the use of the FileChooser class in selecting a data file. The data file, ISRtwoData.txt, lists:
- data title
- applied voltage
- reference impedance
- number of frequencies at which a measurement was made
- a table of the data as rows of frequency in Hz, magnitude of the voltage across the test/model circuit, Vtest, and the phase of the voltage across the test/model circuit, φ.
Example Program Two source code: ExampleProgramTwoImpedRegr.java
OTHER CLASSES USED BY THIS CLASS
This class uses the following classes in this library:
This page was prepared by Dr Michael Thomas Flanagan
|