2021
Authors: C. Zhou and M. R.D. Rodrigues
Journal/Conference: IEEE Transactions on Geoscience and Remote Sensing
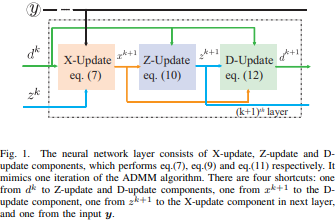
Abstract: Hyperspectral image (HSI) unmixing is an increasingly studied problem in various areas, including remote sensing. It has been tackled using both physical model-based approaches and more recently machine learning-based ones. In this paper, we propose a new HSI unmixing algorithm combining both model- and learning-based techniques, based on algorithm unrolling approaches, delivering improved unmixing performance. Our approach unrolls the Alternating Direction Method of Multipliers (ADMM) solver of a constrained sparse regression problem underlying a linear mixture model. We then propose a neural network structure for abundance estimation that can be trained using supervised learning techniques based on a new composite loss function. We also propose another neural network structure for blind unmixing that can be trained using unsupervised learning techniques. Our proposed networks are also shown to possess a lighter and richer structure containing less learnable parameters and more skip connections compared with other competing architectures. Extensive experiments show that the proposed methods can achieve much faster convergence and better performance even with a very small training dataset size when compared with other unmixing methods such as MNN-AE&BU, UnDIP and EGU-Net.
LinkAuthors: J. Xu, B. Ai, W. Chen, A. Yang, P. Sun, and M. R. D. Rodrigues
Journal/Conference: IEEE Transactions on Circuits and Systems for Video Technology
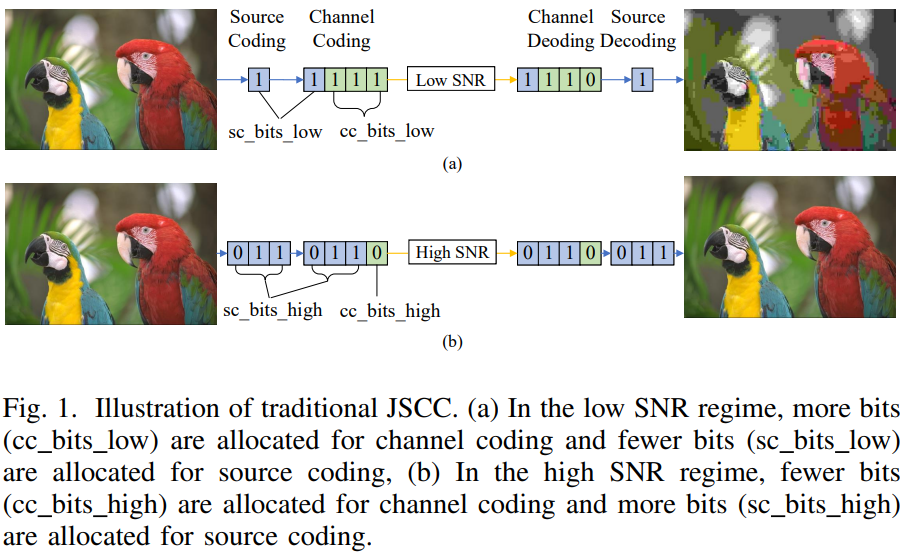
Abstract: Recent research on joint source channel coding (JSCC) for wireless communications has achieved great success owing to the employment of deep learning (DL). However, the existing work on DL based JSCC usually trains the designed network to operate under a specific signal-to-noise ratio (SNR) regime, without taking into account that the SNR level during the deployment stage may differ from that during the training stage. A number of networks are required to cover the scenario with a broad range of SNRs, which is computational inefficiency (in the training stage) and requires large storage. To overcome these drawbacks our paper proposes a novel method called Attention DL based JSCC (ADJSCC) that can successfully operate with different SNR levels during transmission. This design is inspired by the resource assignment strategy in traditional JSCC, which dynamically adjusts the compression ratio in source coding and the channel coding rate according to the channel SNR. This is achieved by resorting to attention mechanisms because these are able to allocate computing resources to more critical tasks. Instead of applying the resource allocation strategy in traditional JSCC, the ADJSCC uses the channel-wise soft attention to scaling features according to SNR conditions. We compare the ADJSCC method with the state-of-the-art DL based JSCC method through extensive experiments to demonstrate its adaptability, robustness and versatility. Compared with the existing methods, the proposed method takes less storage and is more robust in the presence of channel mismatch.
LinkAuthors: J. Amjad, Z. Lyu, and M. R. D. Rodrigues
Journal/Conference: IEEE Transactions on Signal Processing
Abstract: There are various inverse problems – including reconstruction problems arising in medical imaging - where one is often aware of the forward operator that maps variables of interest to the observations. It is therefore natural to ask whether such knowledge of the forward operator can be exploited in deep learning approaches increasingly used to solve inverse problems. In this paper, we provide one such way via an analysis of the generalisation error of deep learning approaches to inverse problems. In particular, by building on the algorithmic robustness framework, we offer a generalisation error bound that encapsulates key ingredients associated with the learning problem such as the complexity of the data space, the size of the training set, the Jacobian of the deep neural network and the Jacobian of the composition of the forward operator with the neural network. We then propose a ‘plug-and-play’ regulariser that leverages the knowledge of the forward map to improve the generalization of the network. We likewise also use a new method allowing us to tightly upper bound the Jacobians of the relevant operators that is much more computationally efficient than existing ones. We demonstrate the efficacy of our model-aware regularised deep learning algorithms against other state-of-the-art approaches on inverse problems involving various sub-sampling operators such as those used in classical compressed sensing tasks, image super-resolution problems and accelerated Magnetic Resonance Imaging (MRI) setups.
LinkAuthors: G. Aminian, Y. Bu, L. Toni, M. R. D. Rodrigues, and G. Wornell
Journal/Conference: Neural Information Processing Systems (NeurIPS)
Abstract: Recent research on joint source channel coding (JSCC) for wireless communications has achieved great success owing to the employment of deep learning (DL). However, the existing work on DL based JSCC usually trains the designed network to operate under a specific signal-to-noise ratio (SNR) regime, without taking into account that the SNR level during the deployment stage may differ from that during the training stage. A number of networks are required to cover the scenario with a broad range of SNRs, which is computational inefficiency (in the training stage) and requires large storage. To overcome these drawbacks our paper proposes a novel method called Attention DL based JSCC (ADJSCC) that can successfully operate with different SNR levels during transmission. This design is inspired by the resource assignment strategy in traditional JSCC, which dynamically adjusts the compression ratio in source coding and the channel coding rate according to the channel SNR. This is achieved by resorting to attention mechanisms because these are able to allocate computing resources to more critical tasks. Instead of applying the resource allocation strategy in traditional JSCC, the ADJSCC uses the channel-wise soft attention to scaling features according to SNR conditions. We compare the ADJSCC method with the state-of-the-art DL based JSCC method through extensive experiments to demonstrate its adaptability, robustness and versatility. Compared with the existing methods, the proposed method takes less storage and is more robust in the presence of channel mismatch.
LinkAuthors: N. Martinez, M. A. Bertran, A. Papadaki, M. R. D. Rodrigues, and G. Sapiro
Journal/Conference: International Conference on Machine Learning (ICML)
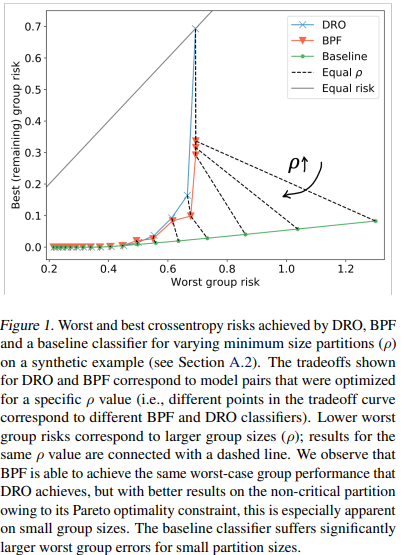
Abstract: Much of the work in the field of group fairness addresses disparities between predefined groups based on protected features such as gender, age, and race, which need to be available at train, and often also at test, time. These approaches are static and retrospective, since algorithms designed to protect groups identified a priori cannot anticipate and protect the needs of different at-risk groups in the future. In this work we analyze the space of solutions for worst-case fairness beyond demographics, and propose Blind Pareto Fairness (BPF), a method that leverages no-regret dynamics to recover a fair minimax classifier that reduces worst-case risk of any potential subgroup of sufficient size, and guarantees that the remaining population receives the best possible level of service. BPF addresses fairness beyond demographics, that is, it does not rely on predefined notions of at-risk groups, neither at train nor at test time. Our experimental results show that the proposed framework improves worst-case risk in multiple standard datasets, while simultaneously providing better levels of service for the remaining population.
LinkAuthors: M. Ferianc, P. Maji, M. Mattina, and M. R. D. Rodrigues
Journal/Conference: Conference on Uncertainty in Artificial Intelligence (UAI)
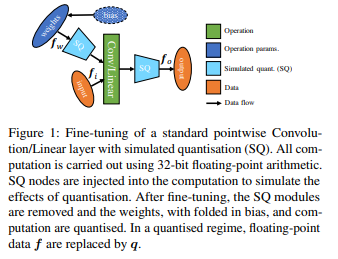
Abstract: Bayesian neural networks (BNNs) are making significant progress in many research areas where decision-making needs to be accompanied by uncertainty estimation. Being able to quantify uncertainty while making decisions is essential for understanding when the model is over-/under-confident, and hence BNNs are attracting interest in safety-critical applications, such as autonomous driving, healthcare, and robotics. Nevertheless, BNNs have not been as widely used in industrial practice, mainly because of their increased memory and compute costs. In this work, we investigate quantisation of BNNs by compressing 32-bit floating-point weights and activations to their integer counterparts, that has already been successful in reducing the compute demand in standard pointwise neural networks. We study three types of quantised BNNs, we evaluate them under a wide range of different settings, and we empirically demonstrate that a uniform quantisation scheme applied to BNNs does not substantially decrease their quality of uncertainty estimation.
Link2020
Authors: M. Zamani, J. Sokolic, D. Jiang, F. Renna, M. R. D. Rodrigues, and A. Demosthenous
Journal/Conference: IEEE Transactions on Biomedical Circuits and Systems
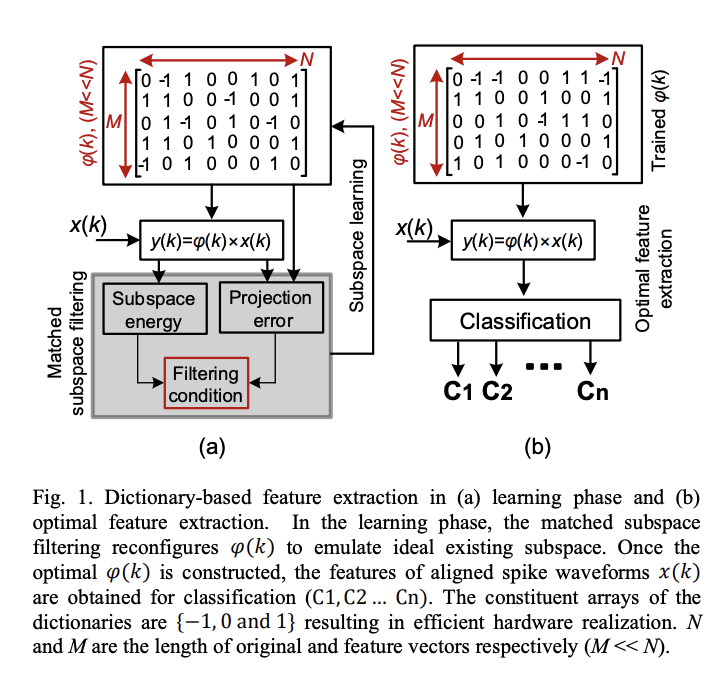
Abstract: This paper presents an adaptable dictionary-based feature extraction approach for spike sorting offering high accuracy and low computational complexity for implantable applications. It extracts and learns identifiable features from evolving subspaces through matched unsupervised subspace filtering. To provide compatibility with the strict constraints in implantable devices such as the chip area and power budget, the dictionary contains arrays of { −1,0 and 1 and the algorithm need only process addition and subtraction operations. Three types of such dictionary were considered. To quantify and compare the performance of the resulting three feature extractors with existing systems, a neural signal simulator based on several different libraries was developed. For noise levels σN between 0.05 and 0.3 and groups of 3 to 6 clusters, all three feature extractors provide robust high performance with average classification errors of less than 8% over five iterations, each consisting of 100 generated data segments. To our knowledge, the proposed adaptive feature extractors are the first able to classify reliably 6 clusters for implantable applications. An ASIC implementation of the best performing dictionary-based feature extractor was synthesized in a 65-nm CMOS process. It occupies an area of 0.09 mm2 and dissipates up to about 10.48 μW from a 1 V supply voltage, when operating with 8-bit resolution at 30 kHz operating frequency.
LinkAuthors: Z. Sabetsarvestani, F. Renna, F. Kiraly and M. R. D. Rodrigues
Journal/Conference: IEEE Transactions on Signal Processing
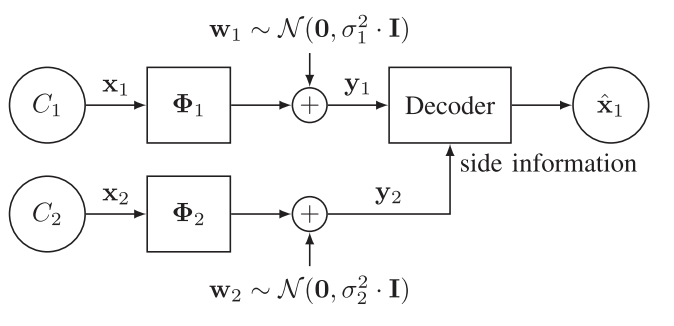
Abstract: n this paper, we propose an algorithm for source separation with side information where one observes the linear superposition of two source signals plus two additional signals that are correlated with the mixed ones. Our algorithm is based on two ingredients: first, we learn a Gaussian mixture model (GMM) for the joint distribution of a source signal and the corresponding correlated side information signal; second, we separate the signals using standard computationally efficient conditional mean estimators. The paper also puts forth new recovery guarantees for this source separation algorithm. In particular, under the assumption that the signals can be perfectly described by a GMM model, we characterize necessary and sufficient conditions for reliable source separation in the asymptotic regime of low-noise as a function of the geometry of the underlying signals and their interaction. It is shown that if the subspaces spanned by the innovation components of the source signals with respect to the side information signals have zero intersection, provided that we observe a certain number of linear measurements from the mixture, then we can reliably separate the sources; otherwise we cannot. Our proposed framework – which provides a new way to incorporate side information to aid the solution of source separation problems where the decoder has access to linear projections of superimposed sources and side information – is also employed in a real-world art investigation application involving the separation of mixtures of X-ray images. The simulation results showcase the superiority of our algorithm against other state-of-the-art algorithms.
LinkAuthors: Rodrigues, M. R. D. and Eldar, Y. C.
Journal/Conference: Cambridge University Press
Abstract: Learn about the state-of-the-art at the interface between information theory and data science with this first unified treatment of the subject. Written by leading experts in a clear, tutorial style, and using consistent notation and definitions throughout, it shows how information-theoretic methods are being used in data acquisition, data representation, data analysis, and statistics and machine learning. Coverage is broad, with chapters on signal acquisition, data compression, compressive sensing, data communication, representation learning, emerging topics in statistics, and much more. Each chapter includes a topic overview, definition of the key problems, emerging and open problems, and an extensive reference list, allowing readers to develop in-depth knowledge and understanding. Providing a thorough survey of the current research area and cutting-edge trends, this is essential reading for graduate students and researchers working in information theory, signal processing, machine learning, and statistics.
Link2019
Authors: Z. Sabetsarvestani, B. Sober, C. Higgitt, I. Daubechies, M. R. D. Rodrigues
Journal/Conference: Science Advances
Abstract: X-ray images of polyptych wings, or other artworks painted on both sides of their support, contain in one image content from both paintings, making them difficult for experts to “read.” To improve the utility of these x-ray images in studying these artworks, it is desirable to separate the content into two images, each pertaining to only one side. This is a difficult task for which previous approaches have been only partially successful. Deep neural network algorithms have recently achieved remarkable progress in a wide range of image analysis and other challenging tasks. We, therefore, propose a new self-supervised approach to this x-ray separation, leveraging an available convolutional neural network architecture; results obtained for details from the Adam and Eve panels of the Ghent Altarpiece spectacularly improve on previous attempts.
LinkAuthors: P. Song, X. Deng, J. F. C. Mota, N. Deligiannis, P.-L. Dragotti, and M. R. D. Rodrigues
Journal/Conference: IEEE Transactions on Computational Imaging
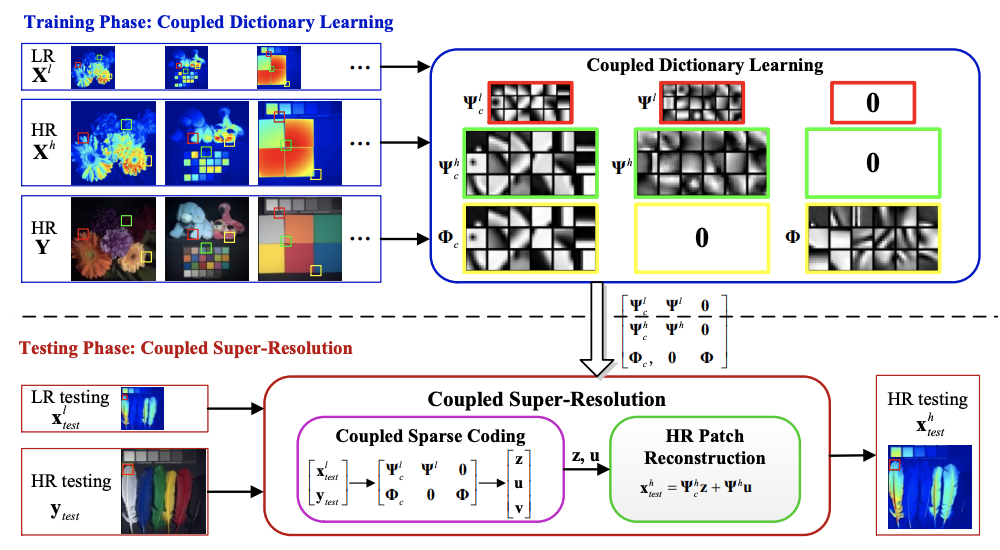
Abstract: Real-world data processing problems often involve various image modalities associated with a certain scene, including RGB images, infrared images or multi-spectral images. The fact that different image modalities often share certain attributes, such as edges, textures and other structure primitives, represents an opportunity to enhance various image processing tasks. This paper proposes a new approach to construct a high-resolution (HR) version of a low-resolution (LR) image given another HR image modality as guidance, based on joint sparse representations induced by coupled dictionaries. The proposed approach captures complex dependency correlations, including similarities and disparities, between different image modalities in a learned sparse feature domain in lieu of the original image domain. It consists of two phases: coupled dictionary learning phase and coupled super-resolution phase. The learning phase learns a set of dictionaries from the training dataset to couple different image modalities together in the sparse feature domain. In turn, the super-resolution phase leverages such dictionaries to construct a HR version of the LR target image with another related image modality for guidance. In the advanced version of our approach, multi-stage strategy and neighbourhood regression concept are introduced to further improve the model capacity and performance. Extensive guided image super-resolution experiments on real multimodal images demonstrate that the proposed approach admits distinctive advantages with respect to the state-of-the-art approaches, for example, overcoming the texture copying artifacts commonly resulting from inconsistency between the guidance and target images. Of particular relevance, the proposed model demonstrates much better robustness than competing deep models in a range of noisy scenarios.
LinkAuthors: X. Deng, P. Song, M. R. D. Rodrigues, and P.-L. Dragotti
Journal/Conference: IEEE Transactions on Circuits and Systems for Video Technology
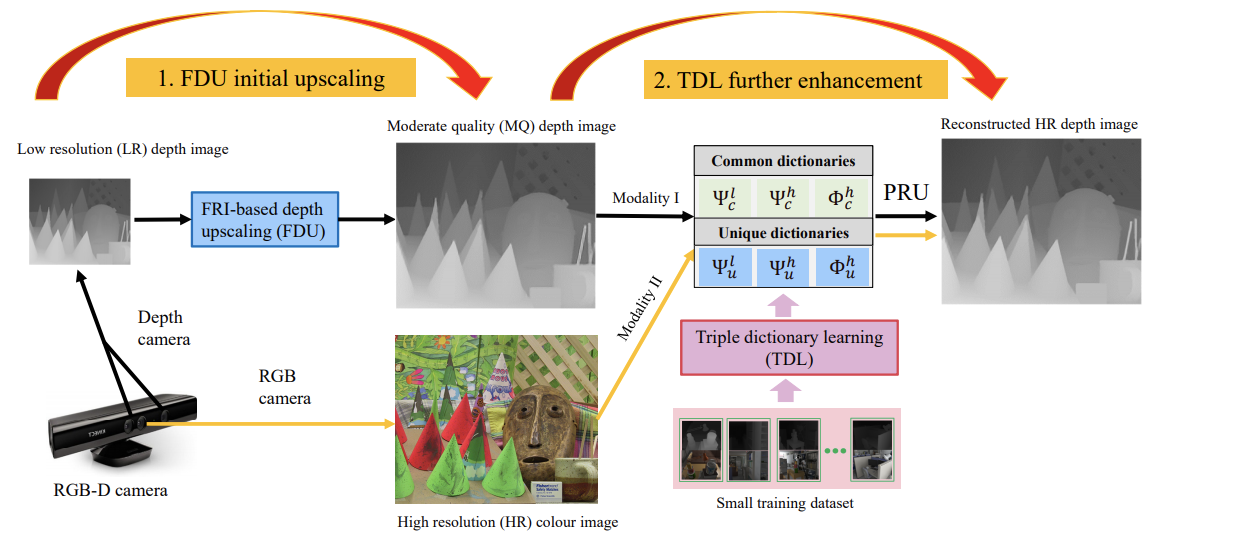
Abstract: Depth image super-resolution is a challenging problem, since normally high upscaling factors are required (e.g., 16×), and depth images are often noisy. In order to achieve large upscaling factors and resilience to noise, we propose a Robust Algorithm for Depth imAge super Resolution (RADAR) that combines the power of finite rate of innovation (FRI) theory with multimodal dictionary learning. Given a low-resolution (LR) depth image, we first model its rows and columns as piece-wise polynomials and propose a FRI-based depth upscaling (FDU) algorithm to super-resolve the image. Then, the upscaled moderate quality (MQ) depth image is further enhanced with the guidance of a registered high-resolution (HR) intensity image. This is achieved by learning multimodal mappings from the joint MQ depth and HR intensity pairs to the HR depth, through a recently proposed triple dictionary learning (TDL) algorithm. Moreover, to speed up the super-resolution process, we introduce a new projection-based rapid upscaling (PRU) technique that pre-calculates the projections from the joint MQ depth and HR intensity pairs to the HR depth. Compared with state-of-the-art deep learning based methods, our approach has two distinct advantages: we need a fraction of training data but can achieve the best performance, and we are resilient to mismatches between training and testing datasets. Extensive numerical results show that the proposed method outperforms other state-of-the-art methods on either noise-free or noisy datasets with large upscaling factors up to 16× and can handle unknown blurring kernels well.
LinkAuthors: N. Shlezinger, Y. C. Eldar, and M. R. D. Rodrigues
Journal/Conference: IEEE Transactions on Signal Processing
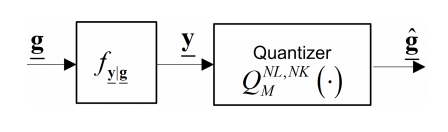
Abstract: Quantizers take part in nearly every digital signal processing system which operates on physical signals. They are commonly designed to accurately represent the underlying signal, regardless of the specific task to be performed on the quantized data. In systems working with high-dimensional signals, such as massive multiple-input multiple-output (MIMO) systems, it is beneficial to utilize low-resolution quantizers, due to cost, power, and memory constraints. In this work we study quantization of high-dimensional inputs, aiming at improving performance under resolution constraints by accounting for the system task in the quantizers design. We focus on the task of recovering a desired signal statistically related to the high-dimensional input, and analyze two quantization approaches: We first consider vector quantization, which is typically computationally infeasible, and characterize the optimal performance achievable with this approach. Next, we focus on practical systems which utilize hardware-limited scalar uniform analog-to-digital converters (ADCs), and design a taskbased quantizer under this model. The resulting system accounts for the task by linearly combining the observed signal into a lower dimension prior to quantization. We then apply our proposed technique to channel estimation in massive MIMO networks. Our results demonstrate that a system utilizing low-resolution scalar ADCs can approach the optimal channel estimation performance by properly accounting for the task in the system design.
LinkAuthors: N. Shlezinger, Y. C. Eldar, and M. R. D. Rodrigues
Journal/Conference: IEEE Transactions on Signal Processing
Abstract: Quantization plays a critical role in digital signal processing systems. Quantizers are typically designed to obtain an accurate digital representation of the input signal, operating independently of the system task, and are commonly implemented using serial scalar analog-to-digital converters (ADCs). In this work, we study hardware-limited task-based quantization, where a system utilizing a serial scalar ADC is designed to provide a suitable representation in order to allow the recovery of a parameter vector underlying the input signal. We propose hardware-limited task-based quantization systems for a fixed and finite quantization resolution, and characterize their achievable distortion. We then apply the analysis to the practical setups of channel estimation and eigen-spectrum recovery from quantized measurements. Our results illustrate that properly designed hardware-limited systems can approach the optimal performance achievable with vector quantizers, and that by taking the underlying task into account, the quantization error can be made negligible with a relatively small number of bits.
LinkAuthors: P. Song, L. Weizmann, J. M. C. Mota, Y. Eldar, and M. R. D. Rodrigues
Journal/Conference: IEEE Transactions on Medical Imaging
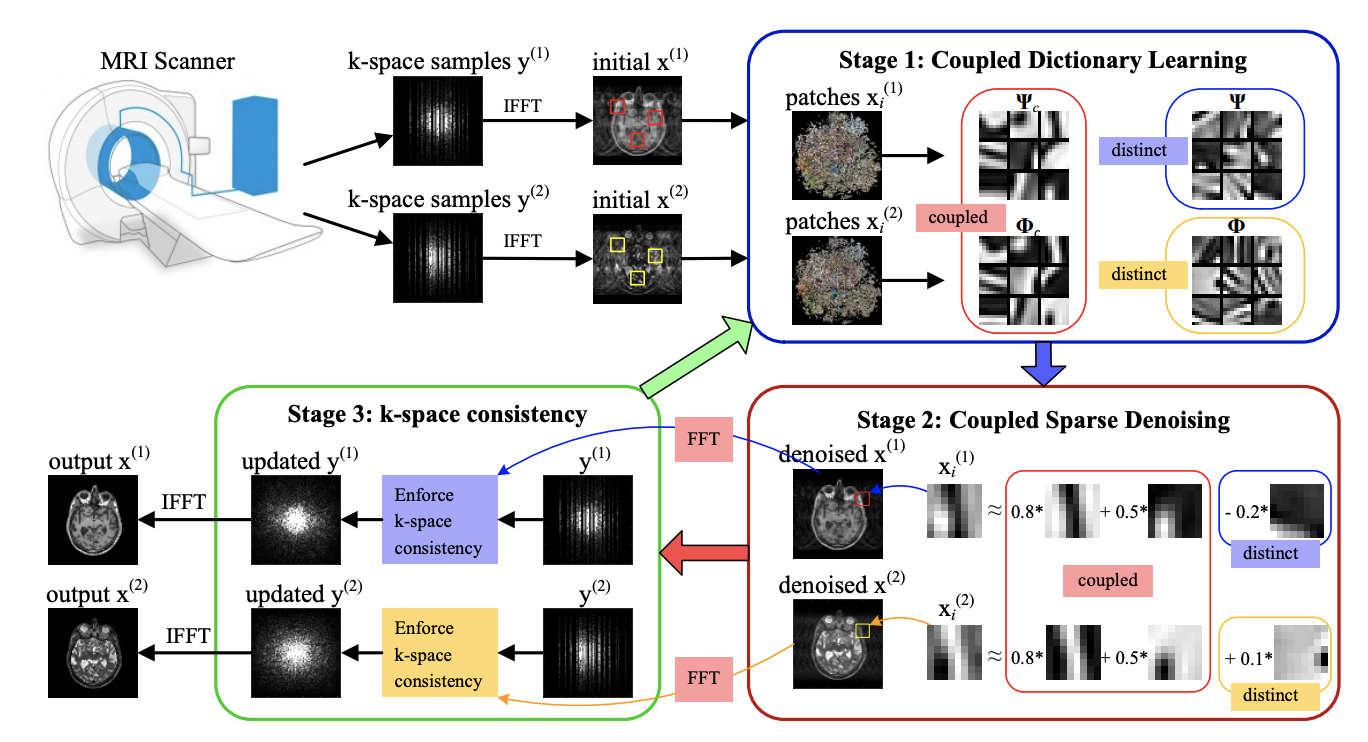
Abstract: Magnetic resonance (MR) imaging tasks often involve multiple contrasts, such as T1-weighted, T2-weighted and Fluid-attenuated inversion recovery (FLAIR) data. These contrasts capture information associated with the same underlying anatomy and thus exhibit similarities in either structure level or gray level. In this paper, we propose a Coupled Dictionary Learning based multi-contrast MRI reconstruction (CDLMRI) approach to leverage the dependency correlation between different contrasts for guided or joint reconstruction from their under-sampled k-space data. Our approach iterates between three stages: coupled dictionary learning, coupled sparse denoising, and enforcing k-space consistency. The first stage learns a set of dictionaries that not only are adaptive to the contrasts, but also capture correlations among multiple contrasts in a sparse transform domain. By capitalizing on the learned dictionaries, the second stage performs coupled sparse coding to remove the aliasing and noise in the corrupted contrasts. The third stage enforces consistency between the denoised contrasts and the measurements in the k-space domain. Numerical experiments, consisting of retrospective under-sampling of various MRI contrasts with a variety of sampling schemes, demonstrate that CDLMRI is capable of capturing structural dependencies between different contrasts. The learned priors indicate notable advantages in multi-contrast MR imaging and promising applications in quantitative MR imaging such as MR fingerprinting.
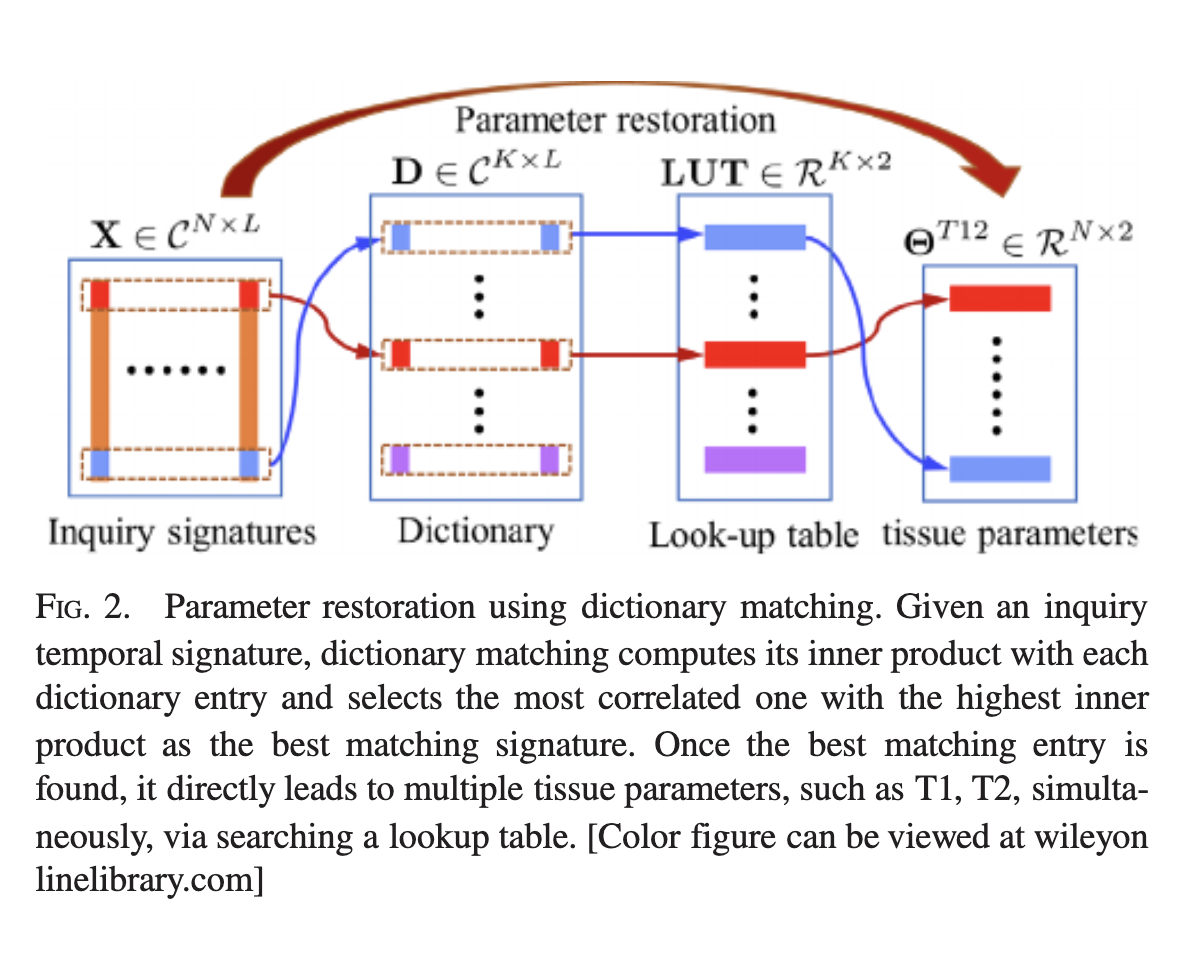
LinkAuthors: P. Song, G. Mazor, Y. C. Eldar, and M. R. D. Rodrigues
Journal/Conference: Medical Physics
Abstract: PURPOSE:
Magnetic resonance fingerprinting (MRF) methods typically rely on dictionary matching to map the
temporal MRF signals to quantitative tissue parameters. Such approaches suffer from inherent
discretization errors, as well as high computational complexity as the dictionary size grows. To
alleviate these issues, we propose a HYbrid Deep magnetic ResonAnce fingerprinting (HYDRA) approach,
referred to as HYDRA.
METHODS:
HYDRA involves two stages: a model-based signature restoration phase and a learning-based parameter
restoration phase. Signal restoration is implemented using low-rank based de-aliasing techniques
while
parameter restoration is performed using a deep nonlocal residual convolutional neural network. The
designed network is trained on synthesized MRF data simulated with the Bloch equations and fast
imaging with steady-state precession (FISP) sequences. In test mode, it takes a temporal MRF signal
as
input and produces the corresponding tissue parameters.
RESULTS:
We validated our approach on both synthetic data and anatomical data generated from a healthy
subject.
The results demonstrate that, in contrast to conventional dictionary matching-based MRF techniques,
our approach significantly improves inference speed by eliminating the time-consuming dictionary
matching operation, and alleviates discretization errors by outputting continuous-valued parameters.
We further avoid the need to store a large dictionary, thus reducing memory requirements.
CONCLUSIONS:
Our approach demonstrates advantages in terms of inference speed, accuracy, and storage requirements
over competing MRF methods.
Authors: M. A. Bertran, N. Martinez, A. Papadaki, Q. Qiu, M. R. D. Rodrigues, G. Reeves, and G. Sapiro.
Journal/Conference: International Conference on Machine Learning (ICML)
Abstract: Data collection and sharing are pervasive aspects of modern society. This process can either be voluntary, as in the case of a person taking a facial image to unlock his/her phone, or incidental, such as traffic cameras collecting videos on pedestrians. An undesirable side effect of these processes is that shared data can carry information about attributes that users might consider as sensitive, even when such information is of limited use for the task. It is therefore desirable for both data collectors and users to design procedures that minimize sensitive information leakage. Balancing the competing objectives of providing meaningful individualized service levels and inference while obfuscating sensitive information is still an open problem. In this work, we take an information theoretic approach that is implemented as an unconstrained adversarial game between Deep Neural Networks in a principled, data-driven manner. This approach enables us to learn domain-preserving stochastic transformations that maintain performance on existing algorithms while minimizing sensitive information leakage.
Link2018
Authors: Rodrigues, M., Bolcskei, H., Draper, S., Eldar, Y., & Tan, V
Journal/Conference: IEEE Journal on Selected Topics in Signal Processing
Abstract: The twenty papers that are included in this special section explore applications of information theoretic methods to emerging data science problems. In particular, the papers cover a wide range of topics that can broadly be organized into four themes: (1) data acquisition, (2) data analysis and processing, (3) statistics and machine learning, and (4) privacy and fairness.
LinkAuthors: Chen, M., Renna, F., & Rodrigues, M. R. D
Journal/Conference: IEEE Transactions on Signal Processing
Abstract: This paper studies how to optimally capture side information to aid in the reconstruction of high-dimensional signals from low-dimensional random linear and noisy measurements, by assuming that both the signal of interest and the side information signal are drawn from a joint Gaussian mixture model. In particular, we derive sufficient and (occasionally) necessary conditions on the number of linear measurements for the signal reconstruction minimum mean squared error (MMSE) to approach zero in the low-noise regime; moreover, we also derive closed-form linear side information measurement designs for the reconstruction MMSE to approach zero in the low-noise regime. Our designs suggest that a linear projection kernel that optimally captures side information is such that it measures the attributes of side information that are maximally correlated with the signal of interest. A number of experiments both with synthetic and real data confirm that our theoretical results are well aligned with numerical ones. Finally, we offer a case study associated with a panchromatic sharpening (pan sharpening) application in the presence of compressive hyperspectral data that demonstrates that our proposed linear side information measurement designs can lead to reconstruction peak signal-to-noise ratio (PSNR) gains in excess of 2 dB over other approaches in this practical application.
Link2017
Authors: Deligiannis, N., Mota, J. F. C., Zimos, E., & Rodrigues, M. R. D
Journal/Conference: IEEE Transactions on Communications
Abstract: Large-scale data collection by means of wireless sensor network and Internet-of-Things technology poses various challenges in view of the limitations in transmission, computation, and energy resources of the associated wireless devices. Compressive data gathering based on compressed sensing has been proven a well-suited solution to the problem. Existing designs exploit the spatiotemporal correlations among data collected by a specific sensing modality. However, many applications, such as environmental monitoring, involve collecting heterogeneous data that are intrinsically correlated. In this paper, we propose to leverage the correlation from multiple heterogeneous signals when recovering the data from compressive measurements. To this end, we propose a novel recovery algorithm-built upon belief-propagation principles-that leverages correlated information from multiple heterogeneous signals. To efficiently capture the statistical dependencies among diverse sensor data, the proposed algorithm uses the statistical model of copula functions. Experiments with heterogeneous air-pollution sensor measurements show that the proposed design provides significant performance improvements against the state-of-the-art compressive data gathering and recovery schemes that use classical compressed sensing, compressed sensing with side information, and distributed compressed sensing.
LinkAuthors: Sokolic, J., Giryes, R., Sapiro, G., & Rodrigues, M. R. D
Journal/Conference: IEEE Transactions on Signal Processing
Abstract: The generalization error of deep neural networks via their classification margin is studied in this work. Our approach is based on the Jacobian matrix of a deep neural network and can be applied to networks with arbitrary non-linearities and pooling layers, and to networks with different architectures such as feed forward networks and residual networks. Our analysis leads to the conclusion that a bounded spectral norm of the network's Jacobian matrix in the neighbourhood of the training samples is crucial for a deep neural network of arbitrary depth and width to generalize well. This is a significant improvement over the current bounds in the literature, which imply that the generalization error grows with either the width or the depth of the network. Moreover, it shows that the recently proposed batch normalization and weight normalization re-parametrizations enjoy good generalization properties, and leads to a novel network regularizer based on the network's Jacobian matrix. The analysis is supported with experimental results on the MNIST, CIFAR-10, LaRED and ImageNet datasets.
LinkAuthors: Mota, J. F. C., Deligiannis, N., & Rodrigues, M. R. D
Journal/Conference: IEEE Transactions on Information Theory
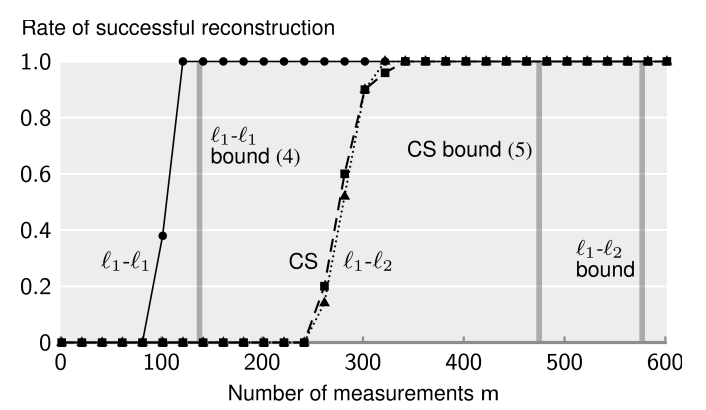
Abstract: We address the problem of compressed sensing (CS) with prior information: reconstruct a target CS signal with the aid of a similar signal that is known beforehand, our prior information. We integrate the additional knowledge of the similar signal into CS via l 1 -l 1 and l 1 -l 2 minimization. We then establish bounds on the number of measurements required by these problems to successfully reconstruct the original signal. Our bounds and geometrical interpretations reveal that if the prior information has good enough quality, l 1 -l 1 minimization improves the performance of CS dramatically. In contrast, l 1 -l 2 minimization has a performance very similar to classical CS, and brings no significant benefits. In addition, we use the insight provided by our bounds to design practical schemes to improve prior information. All our findings are illustrated with experimental results.
LinkAuthors: J. Sokolic, R. Gyries, G. Sapiro, and M. R. D. Rodrigue
Journal/Conference: Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS)
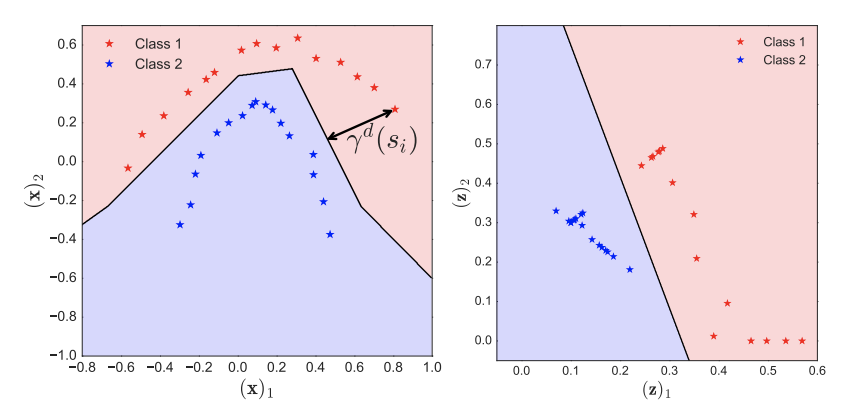
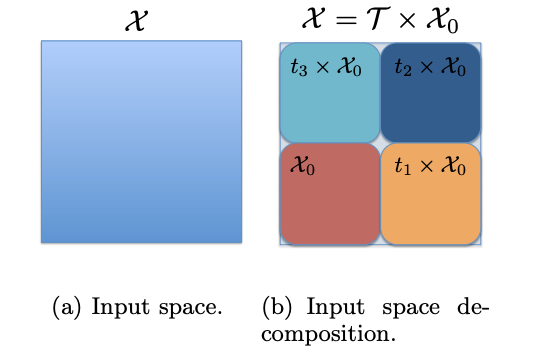
Abstract: This paper studies the generalization error of invariant classifiers. In particular, we consider the common scenario where the classification task is invariant to certain transformations of the input, and that the classifier is constructed (or learned) to be invariant to these transformations. Our approach relies on factoring the input space into a product of a base space and a set of transformations. We show that whereas the generalization error of a non-invariant classifier is proportional to the complexity of the input space, the generalization error of an invariant classifier is proportional to the complexity of the base space. We also derive a set of sufficient conditions on the geometry of the base space and the set of transformations that ensure that the complexity of the base space is much smaller than the complexity of the input space. Our analysis applies to general classifiers such as convolutional neural networks. We demonstrate the implications of the developed theory for such classifiers with experiments on the MNIST and CIFAR-10 datasets.
Link2016
Authors: Renna, F., Wang, L., Yuan, X., Yang, J., Reeves, G., Calderbank, R., Rodrigues, M. R. D
Journal/Conference: IEEE Transactions on Information Theory
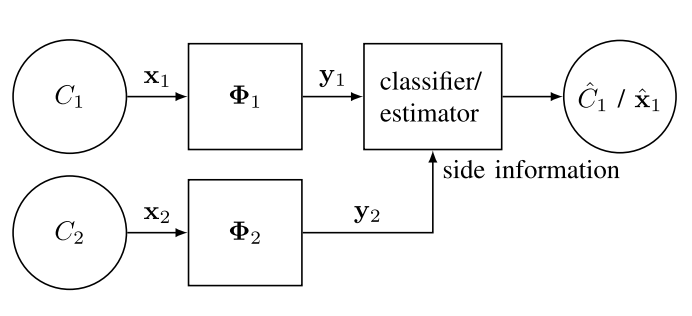
Abstract: This paper offers a characterization of fundamental limits on the classification and reconstruction of high-dimensional signals from low-dimensional features, in the presence of side information. We consider a scenario where a decoder has access both to linear features of the signal of interest and to linear features of the side information signal; while the side information may be in a compressed form, the objective is recovery or classification of the primary signal, not the side information. The signal of interest and the side information are each assumed to have (distinct) latent discrete labels; conditioned on these two labels, the signal of interest and side information are drawn from a multivariate Gaussian distribution that correlates the two. With joint probabilities on the latent labels, the overall signal-(side information) representation is defined by a Gaussian mixture model. By considering bounds to the misclassification probability associated with the recovery of the underlying signal label, and bounds to the reconstruction error associated with the recovery of the signal of interest itself, we then provide sharp sufficient and/or necessary conditions for these quantities to approach zero when the covariance matrices of the Gaussians are nearly low rank. These conditions, which are reminiscent of the well-known Slepian-Wolf and Wyner-Ziv conditions, are the function of the number of linear features extracted from signal of interest, the number of linear features extracted from the side information signal, and the geometry of these signals and their interplay. Moreover, on assuming that the signal of interest and the side information obey such an approximately low-rank model, we derive the expansions of the reconstruction error as a function of the deviation from an exactly low-rank model; such expansions also allow the identification of operational regimes, where the impact of side information on signal reconstruction is most relevant. Our framework, which offers a principled mechanism to integrate side information in high-dimensional data problems, is also tested in the context of imaging applications. In particular, we report state-of-theart results in compressive hyperspectral imaging applications, where the accompanying side information is a conventional digital photograph.
LinkAuthors: Deligiannis, N., Mota, J. F. C., Cornelis, B., Rodrigues, M. R. D., & Daubechies, I.
Journal/Conference: IEEE Transactions on Image Processing
Abstract: In support of art investigation, we propose a new source separation method that unmixes a single X-ray scan acquired from double-sided paintings. In this problem, the X-ray signals to be separated have similar morphological characteristics, which brings previous source separation methods to their limits. Our solution is to use photographs taken from the front-and back-side of the panel to drive the separation process. The crux of our approach relies on the coupling of the two imaging modalities (photographs and X-rays) using a novel coupled dictionary learning framework able to capture both common and disparate features across the modalities using parsimonious representations; the common component captures features shared by the multi-modal images, whereas the innovation component captures modality-specific information. As such, our model enables the formulation of appropriately regularized convex optimization procedures that lead to the accurate separation of the X-rays. Our dictionary learning framework can be tailored both to a single- and a multi-scale framework, with the latter leading to a significant performance improvement. Moreover, to improve further on the visual quality of the separated images, we propose to train coupled dictionaries that ignore certain parts of the painting corresponding to craquelure. Experimentation on synthetic and real data - taken from digital acquisition of the Ghent Altarpiece (1432) - confirms the superiority of our method against the state-of-the-art morphological component analysis technique that uses either fixed or trained dictionaries to perform image separation.
LinkAuthors: Reboredo, H., Renna, F., Calderbank, R., & Rodrigues, M. R. D
Journal/Conference: IEEE Transactions on Signal Processing
Abstract: This paper studies the classification of high-dimensional Gaussian signals from low-dimensional noisy, linear measurements. In particular, it provides upper bounds (sufficient conditions) on the number of measurements required to drive the probability of misclassification to zero in the low-noise regime, both for random measurements and designed ones. Such bounds reveal two important operational regimes that are a function of the characteristics of the source: 1) when the number of classes is less than or equal to the dimension of the space spanned by signals in each class, reliable classification is possible in the low-noise regime by using a one-vs-all measurement design; 2) when the dimension of the spaces spanned by signals in each class is lower than the number of classes, reliable classification is guaranteed in the low-noise regime by using a simple random measurement design. Simulation results both with synthetic and real data show that our analysis is sharp, in the sense that it is able to gauge the number of measurements required to drive the misclassification probability to zero in the low-noise regime.
LinkAuthors: Mota, J. F. C., Deligiannis, N., Sankaranarayanan, A. C., Cevher, V., & Rodrigues, M. R. D.
Journal/Conference: IEEE Transactions on Signal Processing
Abstract: We propose and analyze an online algorithm for reconstructing a sequence of signals from a limited number of linear measurements. The signals are assumed sparse, with unknown support, and evolve over time according to a generic nonlinear dynamical model. Our algorithm, based on recent theoretical results for l1 - l1 minimization, is recursive and computes the number of measurements to be taken at each time on-the-fly. As an example, we apply the algorithm to online compressive video foreground extraction, a problem stated as follows: given a set of measurements of a sequence of images with a static background, simultaneously reconstruct each image while separating its foreground from the background. The performance of our method is illustrated on sequences of real images. We observe that it allows a dramatic reduction in the number of measurements or reconstruction error with respect to state-of-the-art compressive background subtraction schemes.
LinkAuthors: Wang, L., Chen, M., Rodrigues, M., Wilcox, D., Calderbank, R., & Carin, L.
Journal/Conference: IEEE Transactions on Pattern Analysis and Machine Intelligence
Abstract: An information-theoretic projection design framework is proposed, of interest for feature design and compressive measurements. Both Gaussian and Poisson measurement models are considered. The gradient of a proposed information-theoretic metric (ITM) is derived, and a gradient-descent algorithm is applied in design; connections are made to the information bottleneck. The fundamental solution structure of such design is revealed in the case of a Gaussian measurement model and arbitrary input statistics. This new theoretical result reveals how ITM parameter settings impact the number of needed projection measurements, with this verified experimentally. The ITM achieves promising results on real data, for both signal recovery and classification.
LinkAuthors: Sokolic, J., Renna, F., Calderbank, R., & Rodrigues, M. R. D
Journal/Conference: IEEE Transactions on Signal Processing
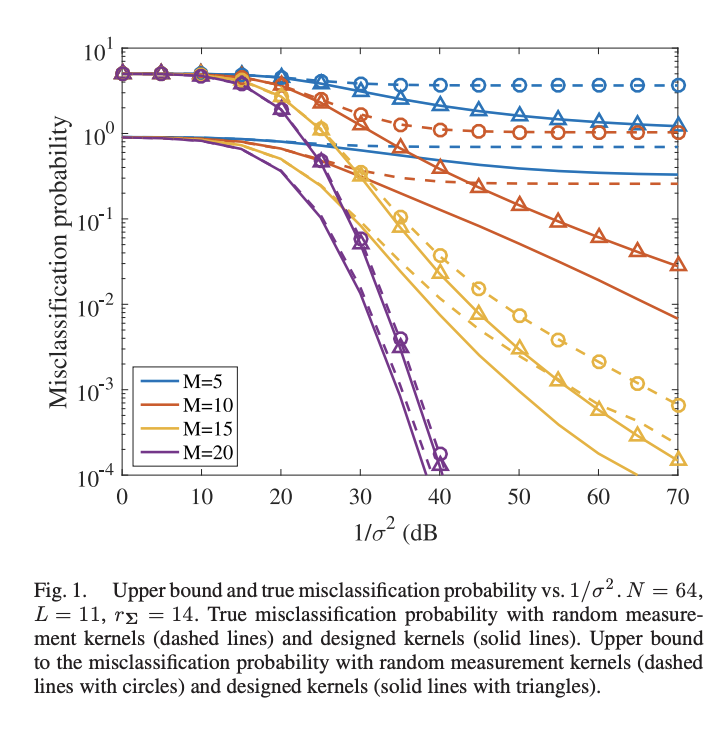
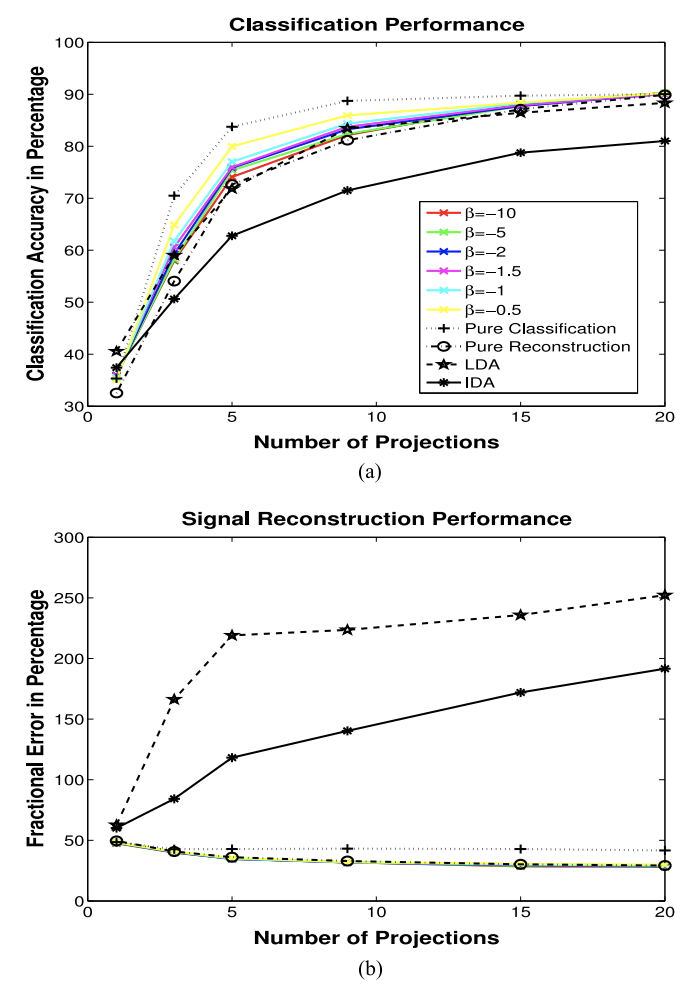
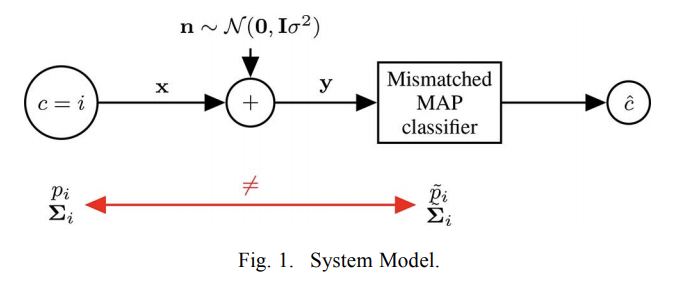
Abstract: This paper considers the classification of linear subspaces with mismatched classifiers. In particular, we assume a model where one observes signals in the presence of isotropic Gaussian noise and the distribution of the signals conditioned on a given class is Gaussian with a zero mean and a low-rank covariance matrix. We also assume that the classifier knows only a mismatched version of the parameters of input distribution in lieu of the true parameters. By constructing an asymptotic low-noise expansion of an upper bound to the error probability of such a mismatched classifier, we provide sufficient conditions for reliable classification in the low-noise regime that are able to sharply predict the absence of a classification error floor. Such conditions are a function of the geometry of the true signal distribution, the geometry of the mismatched signal distributions as well as the interplay between such geometries, namely, the principal angles and the overlap between the true and the mismatched signal subspaces. Numerical results demonstrate that our conditions for reliable classification can sharply predict the behavior of a mismatched classifier both with synthetic data and in a motion segmentation and a hand-written digit classification applications.
LinkAuthors: Sokolic, J., Gyries, R., Sapiro, G., & Rodrigues, M. R. D.
Journal/Conference: International Conference on Learning Representations (ICLR)
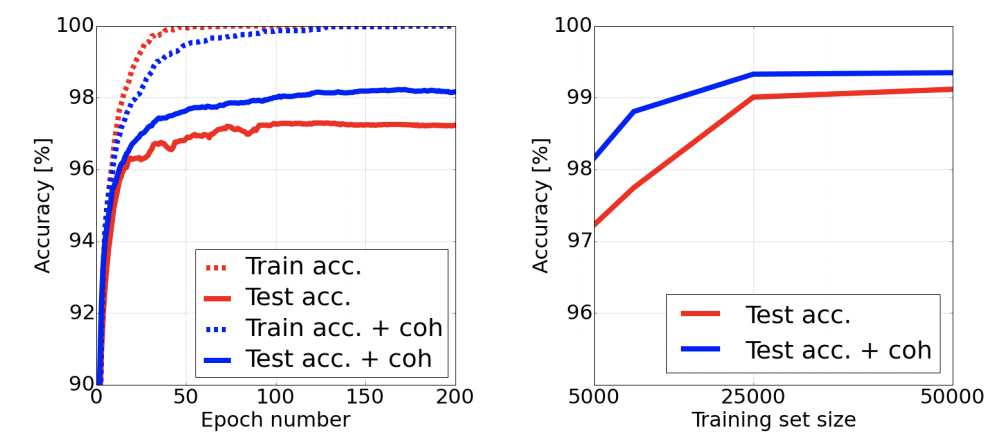
Abstract: Understanding the generalization properties of deep learning models is critical for successful applications, especially in the regimes where the number of training samples is limited. We study the generalization properties of deep neural networks via the empirical Rademacher complexity and show that it is easier to control the complexity of convolutional networks compared to general fully connected networks. In particular, we justify the usage of small convolutional kernels in deep networks as they lead to a better generalization error. Moreover, we propose a representation based regularization method that allows to decrease the generalization error by controlling the coherence of the representation. Experiments on the MNIST dataset support these foundations.
Link