Quantum Computing

Quantum computing was initially proposed as an alternative way of computation to simulate the dynamics of quantum systems, whose computation is exponentially more expensive [1]. The idea then quickly found interest in the academic community and various algorithms and protocols have since then theoretically shown its possible advantages in areas such as finding prime factors of integers, database search and cryptography [2][3][4].

Climate crises, drug and vaccine discovery, financial and economic forecasting, battery improvement, and supply chain solutions; are some of the many areas Quantum Computing is expected to revolutionise in the following decades [5].

Quantum of Quantum Computing

Quantum computing aims to exploit quantum mechanical properties like superposition, interference, and entanglement to achieve "quantum supremacy"—a technological milestone where quantum computers perform computational tasks exponentially faster than classical computers, offering significant advantages in time complexity [6].

To exploit the quantum mechanical properties one requires the experimental realisation of the fundamental block of quantum computing - "Qubits". A classical bit carries the information which can answer a single "yes" or "no" question, utilising "1"s and "0"s [7].

A qubit can be constructed as a superposition of two quantum states, with one representing a classical "0" and the other "1." This superposition implies that each state has a certain probability of being the outcome when the qubit is measured. The qubit can be one of the two, however, we can only associate a probability to each outcome - we do not know what it is until we measure it.

Well, this is a property of quantum mechanics, and to construct such a qubit we require a system exhibiting quantum behaviour. There are several approaches to realise a qubit physically, mainly through [8]:

Atomic, Molecular or Optical Physics (AMO)
Solid State Physics

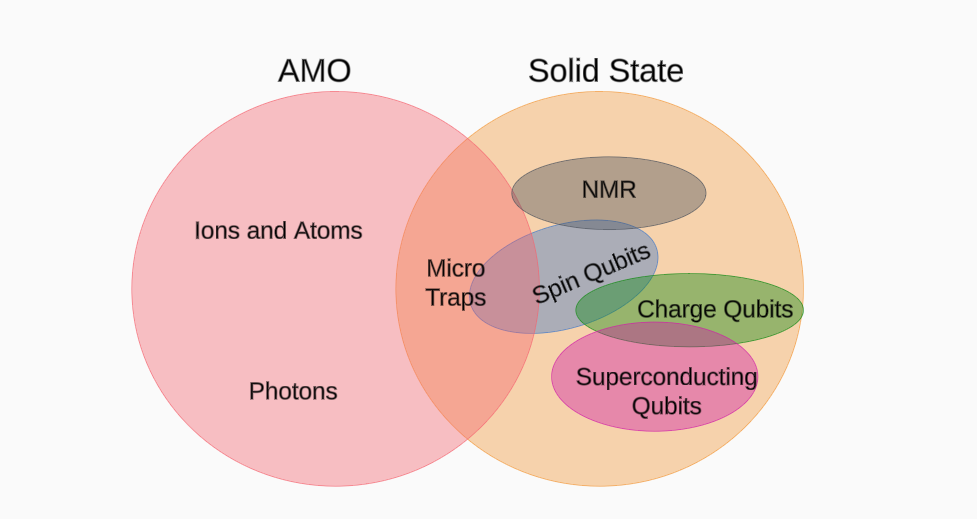
A graphical representation of different approaches to realising qubits. Figure adapted from Ref[8].

The specific technologies for realising qubits can be listed as follows [8]:

Superconductor Based Qubits
Ion Trap Qubits
Neutral Atom Qubits
Quantum Dot Qubits
Photonic Qubits
Topological Qubits
Nuclear Magnetic Resonance (NMR) Qubits

There are various sub-approaches and mixed/hybrid approaches (also with classical computers) utilising the above technologies together to process the quantum information more effectively as there are various areas of strengths and weaknesses [9].

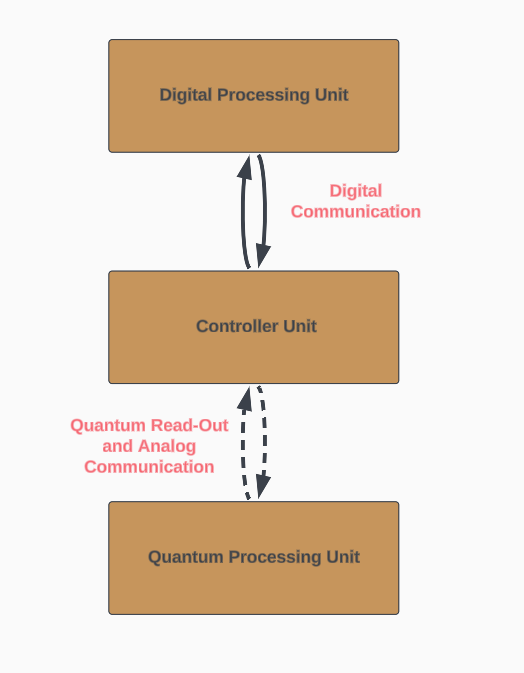
Quantum hardware could be layered into three main sections [10]

The Quantum Processing unit, where qubit processing and quantum memory are realised.
The control unit, where the qubits are operated using analog signals which are created through some previous digital logic. This layer is connected to the quantum processing unit through read-out devices.
The digital processing unit, where the quantum algorithms are executed and communicated to the analog control unit via digital signals.

Within the quantum-classical interface, semiconductor-based quantum and nanoelectronic devices at cryogenic temperatures such as quantum wires could be utilised as read-out and communication devices [11].

Approaches in Quantum Computation X Our Research Interests

Quantum computing could be realised through various computational approaches. Topological, measurement-based, gate-based, and adiabatic quantum computing approaches use various techniques to create, control, and evolve qubits. Here we look at how our research interests and these approaches can overlap.

Topological Quantum Computing

Topological quantum computers aim to utilise non-Abelian anyons for fault-tolerant quantum computation [15]. This specific quantum state of matter allows the protection of quantum information through its physical journey at the hardware level. This intrinsic fault tolerance of topological quantum computation makes it a dark horse in the race to quantum computation, currently seeing more interest from both industry and academia in recent years [16].

Non-Abelian anyons are generated through quasi-particle excitations and are thought to contribute to certain fractional states in the Fractional Quantum Hall Effect [17]. Our research interest includes the investigation of exotic quasi-particle excitations in interacting 1-D and 2-D systems.

Adiabatic Quantum Computing

Adiabatic quantum computation uses quantum annealing to find an energy minimum of possible outcomes of quantum computation in the physical process itself. It is commercially in development using superconducting qubits [20]. It has a fundamentally different working principle than other computational methods and is very promising for its use in optimisation problems. Even though semiconductor-based quantum annealing machines are in the early stages of development, there are proposals for semiconductor quantum dot-based approaches [21].

One-way or Measurement-based Quantum Computing (MBQC)

MBQC operates by initially creating a so-called cluster state of a large number of entangled qubits [12]. The computation is then completed by processing onto the cluster state and making a one-particle measurement. All unitary transformations that could be realised with other universal quantum computation schemes can also be realised through the processing of this entangled state [12]. This approach could be realised through a photonic or a condensed matter system including trapped ions, cold atoms, superconductors and also semiconductor quantum dot systems [13]. The model suggests that if one can manipulate quantum dots on a 2D lattice, by imposing processes such as rotations and nearest-neighbour Ising interactions followed by measurements in the 2D plane - one-way quantum computation could be realised in the 2D plane with many 0-D subsystems [14].

Gate-Based Computing

Gate-based quantum computation could be considered as the most widely adopted approach in quantum computation. Qubits are evolved through unitary transformation realised by local logical operations by "gates". Also known as the quantum circuit model initially introduced by Feynman himself [18].

Two-gate fidelities of above 99% have been reported in semiconductor spin qubits with quantum dots in Si/SiGe heterostructures [19].

References

[1] R. P. Feynman, Simulating Physics with Computers, Int. J. Theor. Phys. 21, 467 (1982). [2] P. W. Shor, Algorithms for quantum computation: discrete logarithms and factoring, Proceedings 35th Annual Symposium on Foundations of Computer Science,124 (1994). [3] L. K. Grover, A fast quantum mechanical algorithm for database search, Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, 212 (1996). [4] C. H. Bennett and G. Brassard, Quantum cryptography: Public key distribution and coin tossing, Theor. Comput. Sci. 560, 7 (2014).[5] S. S. Gill et al., Quantum Computing: A Taxonomy, Systematic Review and Future Directions, Softw: Pract Exper. 52, 66 (2022). [6] J. Preskill, Quantum computing and the entanglement frontier, arXiv:1203.5813v3 (2012). [7] B. Schumacher, Quantum coding, Phys. Rev. A 51, 2738 (1995). [8] H. Bluhm, T. Brückel, M. Morgenstern, G. V. Plessen and C. Stampfer, Electrons in solids: Mesoscopics, photonics, quantum computing, correlations, topology (Walter de Gruyter GmbH, Berlin, 2019). [9] G. Kurizki et al., Quantum technologies with hybrid systems, Proc. Natl. Acad. Sci. U.S.A. 112, 3866 (2015). [10] M. Oskin et al., A practical architecture for reliable quantum computers, Computer 35, 79 (2002). [11] J. Elzerman et al., Few-electron quantum dot circuit with integrated charge read out, Phys. Rev. B 67, 161308 (2003). [12] R. Raussendorf and H. Briegel, A One-Way Quantum Computer, Phys. Rev. Lett. 86, 5188 (2001). [13] R. Raussendorf et al., Topological fault-tolerance in cluster state quantum computation, New J. Phys. 9, 199 (2007). [14] Y. Weinstein et al., Quantum-dot cluster-state computing with encoded qubits, Phys. Rev. A 72, 020304 (2005).[15] J. K. Pachos, Introduction to Topological Quantum Computation (Cambridge University Press, Cambridge, 2012).[16] E. Gibney, Inside Microsoft’s quest for a topological quantum computer, Nature, (2016).[17] S. D. Sarma et al., Topologically protected qubits from a possible non-abelian fractional quantum Hall state, Phys. Rev. Lett. 94, 166802 (2005). [18] R. P. Feynman, Quantum mechanical computers, Found. Phys. 16, 507 (1986). [19] X. Xue et al., Quantum logic with spin qubits crossing the surface code threshold, Nature 601, 343 (2022). [20] M. W. Johnson et al., Quantum annealing with manufactured spins, Nature 473, 194 (2011).[21] T. Tanamoto et al., Quantum Annealing Machines Based on Semiconductor Nanostructures, J. Phys. Soc. Jpn. 88, 061013 (2019).