In classical physics, the motion occurs in a three-dimensional space. To understand a 2D system, we can imagine all particles live in a plane which means that particles do not overlap in z-direction and can only move in two directions. A typical 2D nanostructure is a two-dimensional electron gas and the heterojunction is usually used to form a 2DEG by trapping the electron within a triangle well. The reason for the formation of 2DEG is that once the thickness of the plane becomes appreciably less than the Bohr radius which depends on temperature and other parameters. It is difficult for electrons to tunnel the barrier because of the energy difference between the well and the barrier, and the trapped electron forms a 2DEG.
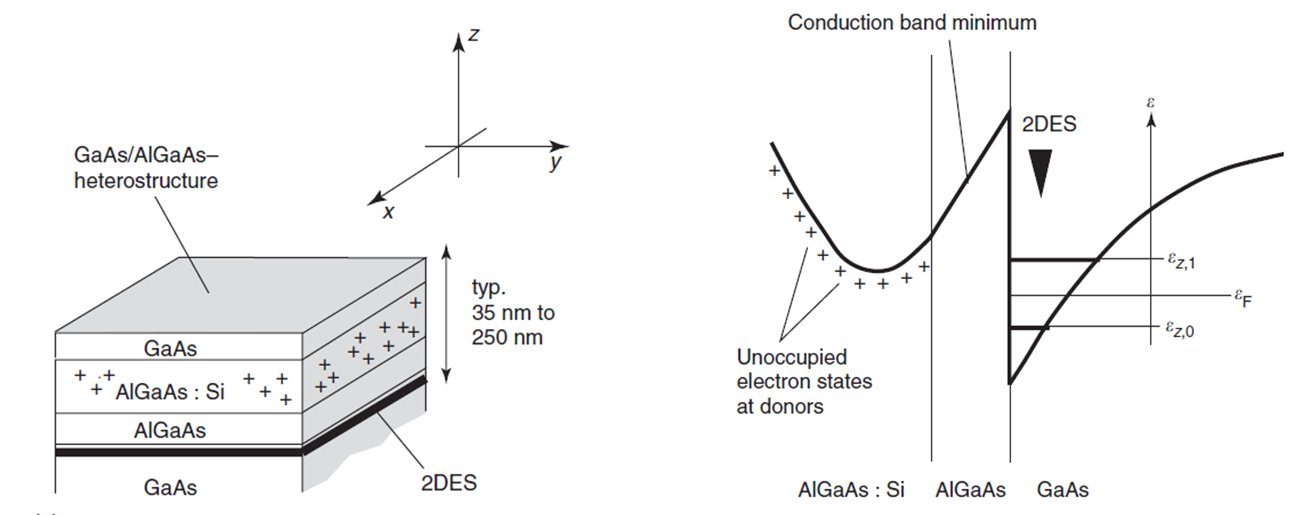
Figure 1: (a) GaAs/AlGaAs heterostructures with a 2DEG at the heterojunction in GaAs. (b) Sketch of the respective profile of the conduction band edge in the z-direction.
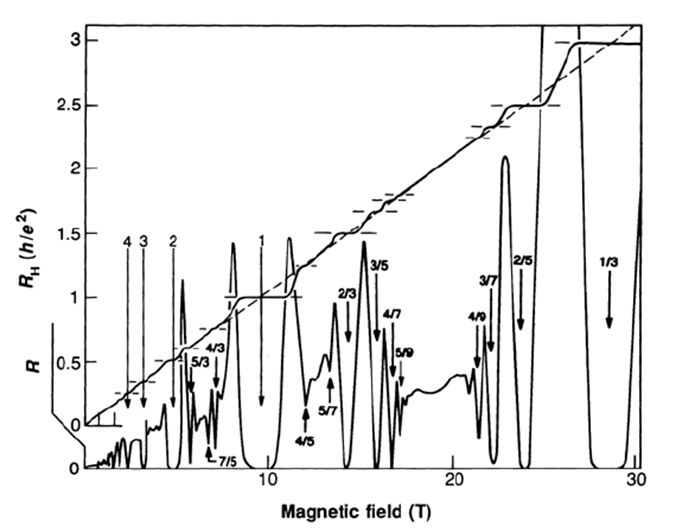
Figure 2: The resistances for the quantum Hall effect, the Hall resistance has a stepwise dependence on the magnetic field and those step resistances are quantized and divided by both integer and fractional values. The longitudinal resistance decreases to zero when the Hall resistance sits on plateaus and shows Shubnikov–de Haas oscillation behaviour.
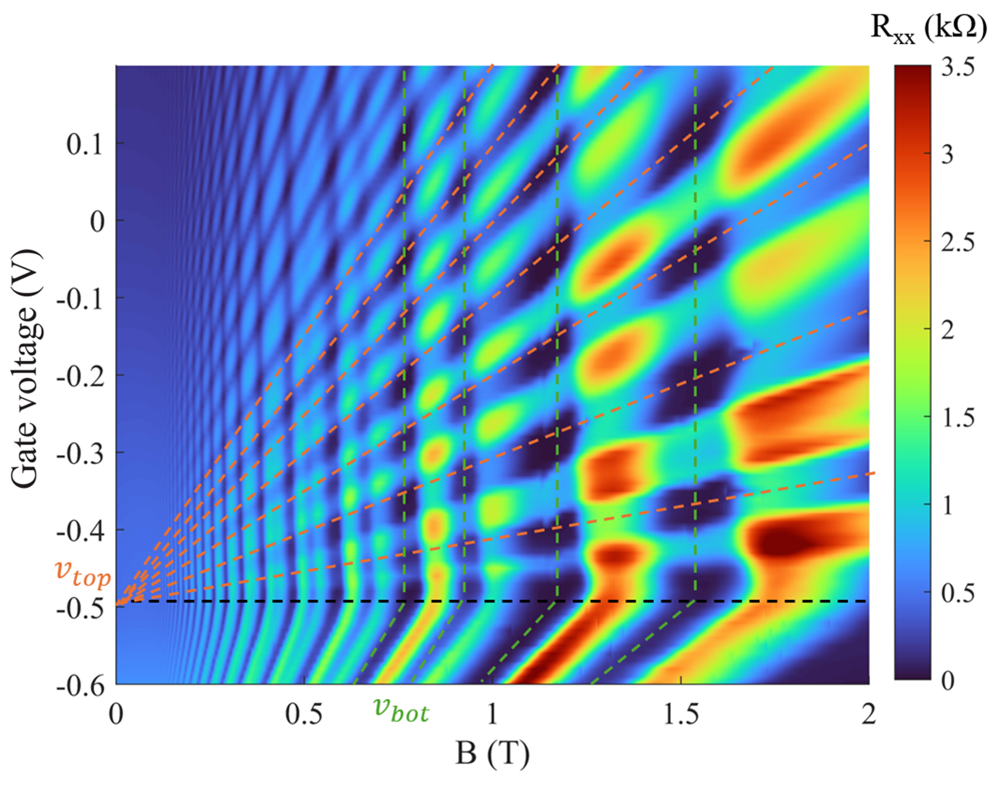
Figure 3: The longitudinal magnetoresistance as a function of magnetic field and top gate voltage measured in our lab.
Low-dimensional nanostructures based on semiconductors offer immense potential for electronic and spintronic applications due to the confinement of electrons and the associated effects. These materials enable the study of quantum phenomena in electron transport, of which the quantum Hall effect (QHE) is one of the most fascinating. In 1980, while working with a silicon metal oxide semiconductor field effect transistor (Si MOSFET), Klaus von Klitzing made a breakthrough discovery for which he was awarded the Nobel Prize in 1985 [1]. This specific manifestation of the quantum Hall effect is known as the integer quantum Hall effect (IQHE). The IQHE is characterized by the Hall resistance exhibiting discrete steps as a function of the magnetic field, with these step resistances quantized as h/e2 divided by an integer value. Subsequently, the fractional quantum Hall effect (FQHE) was observed in the two-dimensional electron gas (2DEG) formed in GaAs/AlGaAs heterostructures [2]. In contrast to IQHE, which results from single particle localization, FQHE arises from electron-electron interactions [3]. GaAs/AlGaAs heterostructures with high mobility provide an ideal experimental environment for the study of correlated 2DEGs [4,5]. Among the various fractional quantum Hall states, the 5/2 state discovered in 1987 stands out as a mysterious anomaly [4]. Prior to its discovery, all other fractional quantum Hall states had odd denominators. This state with an even denominator was the first observed on the second Landau level. The unique topological properties of the 5/2 state make it a promising candidate for topological quantum computation, as it is thought to host anyons—spatially localized quasiparticles with unconventional exchange statistics. Our research target based on 2DEG is to investigate this intriguing 5/2 state in the FQHE to further our understanding of topological phenomena.
References
[1] K. v. Klitzing et al., New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance, Phys. Rev. lett. 45, 494 (1980).
[2] D. C. Tusi et al., Two-dimensional magnetotransport in the extreme quantum limit, Phys. Rev. Lett. 48, 1559 (1982).
[3] R. B. Laughlin, Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations, Phys. Rev. lett. 50, 1395 (1983).
[4] R. Willett et al., Observation of an even-denominator quantum number in the fractional quantum Hall effect, Phys. Rev. lett. 59, 1776 (1987).
[5] R. B. Laughlin, Quantized Hall conductivity in two dimensions, Phys. Rev. B 23, 5632(R) (1981).
