The Excitement
The major problem that quantum computing systems face is an effect called decoherence. Quantum particles are very sensitive and constantly interact with their environment. These interactions can include changes in temperature, interactions with other particles, and even background microwave radiation. This is why solid-state quantum computation must be performed in highly isolated systems, such as in dilution refrigerators. However, even then, these interactions persist and cause "decoherence" in the system; in other words, we lose the information required to complete or continue the quantum computation. To address this issue, a process called quantum error correction is an active and large area of research. Error correction systems aim to utilise additional qubits to recover information affected by decoherence during computation. If we take a step back, the problem becomes apparent: more qubits for error correction lead to greater demand for error correction itself, potentially creating a positive feedback loop where quantum computation may no longer be advantageous. Thus, quantum computing research in both industry and academia has shifted its primary focus to developing systems with inherently low error rates to avoid reaching a point where extensive error correction makes computation inefficient. Topological quantum computation is an idea proposed to solve this issue at the level of computation in the hardware, hence the excitement [1].
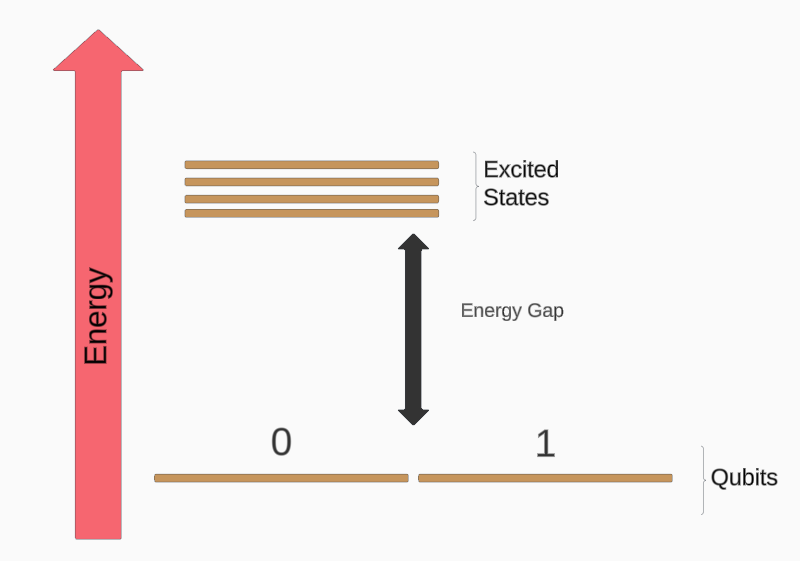
Decoherence arises if the qubits that we want for the computation couples with the excited states during some process. In topological states, one now considers gapped phases with a hidden or protected degenerate ground state in which qubits could be realised. Figure adapted from Ref[6].
Anyons and Topological Quantum Computation
Topological quantum computers use anyons as fundamental building blocks for their operations. In quantum mechanics, there are two main groups of particles governed by different statistics: fermions and bosons. Fermions, such as protons or electrons, cannot occupy the same quantum state, while bosons, like photons and mesons, tend to occupy the same state. Anyons are neither fermions nor bosons; they follow unique statistical rules and can only exist in two-dimensional systems [2].
Anyons are “quasiparticles,” meaning they represent a collective behaviour of particles—usually electrons in condensed matter systems—that together behave like a theoretical particle called an anyon. This collective behaviour allows their properties to be exploited for computation. When well-isolated and with a sufficient energy gap around their interactions, anyons can be put into distinct groups based on their topology, making them suitable for both quantum computation and memory storage [3][4].
Quantum information is encoded in the possible outcomes of the interaction between two anyons when they are brought close together. As they can be grouped and separated from each other due to their topological properties, their unique paths are isolated and therefore the information is protected and hidden. This feature promises fault-tolerant quantum computation at the hardware level, reducing the need for complex error correction [2].
Observing anyons experimentally remains a major area of research. Anyons can be classified into Abelian and non-Abelian types, with the latter believed to be particularly useful for quantum computing [2][3][4]. Non-Abelian anyons are thought to contribute to certain fractional states in the fractional quantum Hall effect [5]. Our research in low-dimensional quantum systems explores these exotic quantum states, focusing on complex many-body interactions and potential systems that could give rise to non-Abelian anyons.
References
[1] E. Gibney, Inside Microsoft’s quest for a topological quantum computer, Nature, (2016).[2] J. K. Pachos, Introduction to Topological Quantum Computation (Cambridge University Press, Cambridge, 2012).[3] A. Y. Kitaev, Fault-tolerant quantum computation by anyons, Ann. Phys. 303, 2 (2003).[4] S. D. Sarma et al., Topologically protected qubits from a possible non-abelian fractional quantum Hall state, Phys. Rev. Lett. 94, 166802 (2005). [5] G. Moore and N. Read, Nonabelions in the fractional quantum Hall effect, Nucl. Phys. B 360, 362 (1991). [6] A. Kitaev and C. Laumann, Topological phases and quantum computation, arXiv:0904.2771v1 (2009).