1-D systems could be realised in different materials, exhibiting different physics or material properties, these can include:
1D structures that are electrostatically defined on the 2DEG, such as quantum point contacts and wires
Semiconductor nanowires
Carbon nanotubes
Nanoribbons
In all cases, if one speaks of experimenting with quantum states, the fundamental principle relies on confinement in two dimensions and freedom of movement in only one direction. Our research primarily focuses on the 1-D systems that are defined and controlled electrostatically on 2DEG in GaAs.
Excotic states in quasi-one-dimensional systems
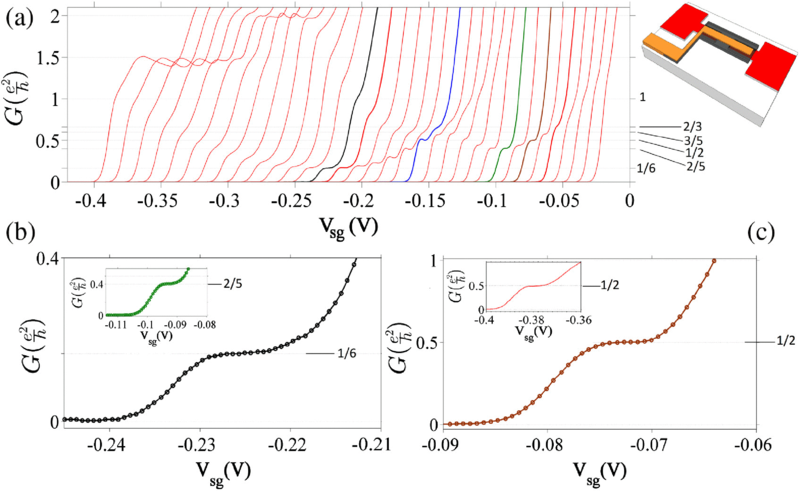
Our group has experimentally observed fractional conductance quantisation under a zero-magnetic field. These experiments utilised a top gate voltage over a quantum wire to control the electron concentration in the channel by depletion through applied negative voltage. The fractional states were observed when the confinement potential was relaxed in the transverse direction, therefore putting the system in a 1D/2D transition regime. It is suggested that such a relaxation results in the formation of a zigzag array of electrons with ring paths which establish a cyclic current and a resultant lowering of energy. The behaviour has been observed for both symmetric and asymmetric confinement but increasing the asymmetry of the confinement potential, to result in a flattening of confinement, enhances the appearance of new fractional states.
Explore our selected publications if you are interested!
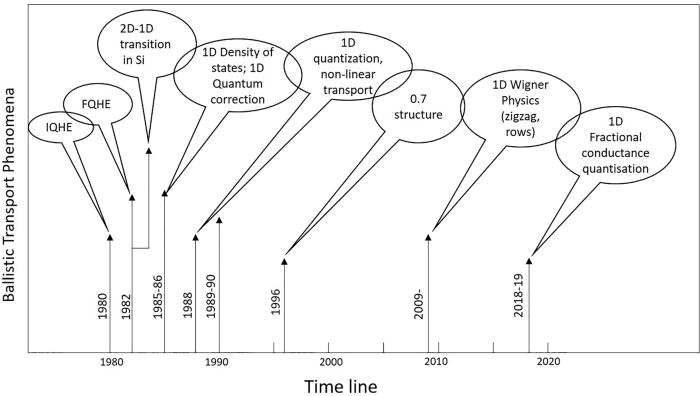
The historical developments in investigating low-dimensional electronic transport phenomena can be seen on the right. Transport measurements are commonly used to investigate the electrical properties of materials. Today, the developments in fabrication technology and the development of high-quality materials allow transport measurements to be used in the research of electronic and quantum behaviour in highly controlled environments. Our interest in fractional quantisation comes from a very fundamental curiosity, to investigate many-body interactions and our ability to control these wavefunctions [1,2].
Image taken from Ref[1]
Some of the primary research points include the investigation of novel quantum phenomena arising from correlation effects in one-dimensional (1D) quantum systems. In a 1D channel with interacting charge carriers, the correlation effects intensify to the point where the system can no longer be well described by conventional Fermi liquid theory. The ground state emerges as a collective excitation of charge carriers, which is well described by the Luttinger liquid theory. This work involves conductance measurements on split-gate-defined 1D wires formed by electrostatic confinement in a two-dimensional electron gas in GaAs/AlGaAs-based heterostructures. Varying the number of charge carriers using a top gate changes the competition between kinetic (Fermi) energy and interaction (Coulomb) energy. Furthermore, changing the confinement symmetry (from symmetric to asymmetric), applying a DC source-drain bias and manipulating spin states under high magnetic fields allow the realisation of intricate quantum states such as fractional states and Wigner crystals.
Another of our research interests includes 1D semiconductor devices based on the Aharanov-Bohm ring geometries. These systems allow the investigation of the quantum interference effects in 1D alongside the investigation of the magnetic field-related effects in such systems.
Conductance characteristics of a top-gated split gate device as a function of asymmetry and width of the confinement potential. Inset on the right side in (a) shows a schematic diagram of the device; split gates are shown in red; PMMA is shown in gray sandwiched between the split gates and the top gate (orange). (a) At 𝑉tg=−0.36 V, the offset or asymmetry between the split gates, Δ𝑉sg was incremented from 0.65 (left) to 0.98 V (right) in steps of 10 mV so widening the channel and flattening the confinement. (b) Main and inset, and (c) show close-up views of fractional states at 1/6, 2/5, and 1/2, respectively, as seen in (a). An inset in (c) shows a close-up of the 1/2 fractional state in a symmetric confinement potential in sample 2 at 𝑉tg=−0.6 V. A horizontal offset of 4 mV was set between the consecutive traces in (a) for clarity.
Image taken from Ref[2]
References
[1] S. Kumar and M. Pepper, Interactions and non-magnetic fractional quantization in one-dimension, Appl. Phys. Lett. 119, 110502 (2021).[2] S. Kumar et al., Zero-Magnetic Field Fractional Quantum States, Phys. Rev. Lett. 122, 086803 (2019).